Řešené úlohy - čtyřúhelníky
Příklad 1
Sestrojte kosočtverec ABCD, znáte-li délky strany a a výšky v (tj. vzdálenost bodu C od úsečky AB).
ŘEŠENÍ
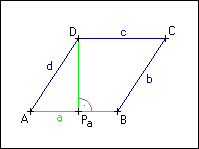
Sestrojte kosočtverec ABCD, znáte-li délky strany a a výšky v (tj. vzdálenost bodu C od úsečky AB).
ŘEŠENÍ
Příklad 2
Sestrojte rovnoběžník ABCD, znáte-li délky strany a, úhlopříčky |BD| = f a velikost úhlu | BSC| = λ, kde S je průsečík úhlopříček.
BSC| = λ, kde S je průsečík úhlopříček.
ŘEŠENÍ
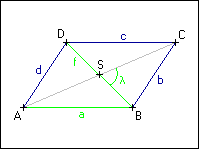
Sestrojte rovnoběžník ABCD, znáte-li délky strany a, úhlopříčky |BD| = f a velikost úhlu |
ŘEŠENÍ
Příklad 3
Sestrojte rovnoramenný lichoběžník ABCD, znáte-li délky základen a, c a velikost vnitřního úhlu | BAD| = α.
BAD| = α.
ŘEŠENÍ
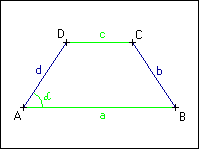
Sestrojte rovnoramenný lichoběžník ABCD, znáte-li délky základen a, c a velikost vnitřního úhlu |
ŘEŠENÍ
Příklad 4
Sestrojte lichoběžník ABCD, znáte-li délky jeho základen a, c a ramen b, d. Předpokládejte a > c.
ŘEŠENÍ
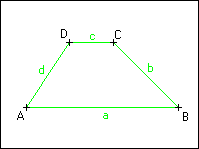
Sestrojte lichoběžník ABCD, znáte-li délky jeho základen a, c a ramen b, d. Předpokládejte a > c.
ŘEŠENÍ
Příklad 5
Sestrojte lichoběžník PQRT, znáte-li délky jeho ramen q, t, jeho úhlopříčky |QT| = f a velikost úhlu | PTQ| = τ.
PTQ| = τ.
ŘEŠENÍ
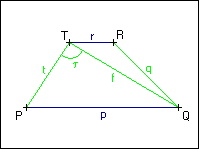
Sestrojte lichoběžník PQRT, znáte-li délky jeho ramen q, t, jeho úhlopříčky |QT| = f a velikost úhlu |
ŘEŠENÍ
Příklad 6
Sestrojte lichoběžník ABCD, znáte-li délky jeho základen a, c, jeho strany d a velikost úhlu | BAC| = ψ.
BAC| = ψ.
ŘEŠENÍ
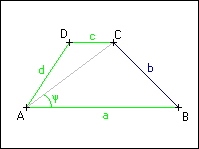
Sestrojte lichoběžník ABCD, znáte-li délky jeho základen a, c, jeho strany d a velikost úhlu |
ŘEŠENÍ
Příklad 7
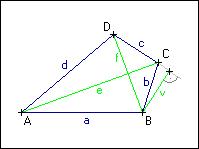
Sestrojte čtyřúhelník ABCD, znáte-li délky jeho stran a, d, jeho úhlopříčky |AC| = e a velikosti úhlů | DBA| = ψ a |
DBA| = ψ a | ADC| = δ.
ADC| = δ.
ŘEŠENÍ
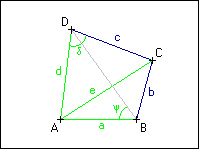
Sestrojte čtyřúhelník ABCD, znáte-li délky jeho stran a, d, jeho úhlopříčky |AC| = e a velikosti úhlů |
ŘEŠENÍ
Příklad 8
Sestrojte čtyřúhelník ABCD, znáte-li délky jeho stran b, c a d a velikosti úhlů |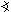 DCB| = γ a úhel σ, který svírají úhlopříčky.
DCB| = γ a úhel σ, který svírají úhlopříčky.
ŘEŠENÍ
Sestrojte čtyřúhelník ABCD, znáte-li délky jeho stran b, c a d a velikosti úhlů |
ŘEŠENÍ
Příklad 9
Sestrojte čtyřúhelník PQRT, znáte-li délky jeho stran q a t a velikosti úhlů | RQP| = ω a |
RQP| = ω a | PTR| = τ a |
PTR| = τ a | PRQ| = ρ.
PRQ| = ρ.
ŘEŠENÍ
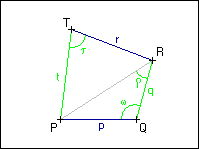
Sestrojte čtyřúhelník PQRT, znáte-li délky jeho stran q a t a velikosti úhlů |
ŘEŠENÍ
Příklad 10
Sestrojte tětivový čtyřúhelník KLMN, znáte-li délky jeho stran k a l, velikost úhlu | MLN| = λ a poloměr kružnice opsané r.
MLN| = λ a poloměr kružnice opsané r.
ŘEŠENÍ
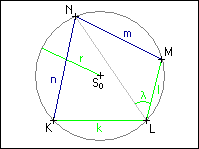
Sestrojte tětivový čtyřúhelník KLMN, znáte-li délky jeho stran k a l, velikost úhlu |
ŘEŠENÍ
Příklad 11
Sestrojte tečnový čtyřúhelník ABCD, znáte-li délky jeho strany a a úhlopříčky f = |BD| a velikosti vnitřních úhlů | BAD| = α a |
BAD| = α a | CBA| = β.
CBA| = β.
ŘEŠENÍ
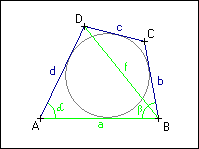
Sestrojte tečnový čtyřúhelník ABCD, znáte-li délky jeho strany a a úhlopříčky f = |BD| a velikosti vnitřních úhlů |
ŘEŠENÍ
Příklad 12
Sestrojte deltoid ABCD, znáte-li délky jeho hlavní úhlopříčky e = |AC| a vedlejší úhlopříčky f = |BD| a vzdálenost v bodu B od strany CD.
ŘEŠENÍ
Sestrojte deltoid ABCD, znáte-li délky jeho hlavní úhlopříčky e = |AC| a vedlejší úhlopříčky f = |BD| a vzdálenost v bodu B od strany CD.
ŘEŠENÍ