Osy stran

Osa úsečky je přímka procházející jejím středem, která je navíc na danou úsečku kolmá. Osu strany trojúhelníka chápeme jako osu úsečky, kde stranu považujeme za úsečku. Například osa strany AB je kolmice na AB vedená středem S_AB. Je to přímka, pro jejíž body platí, že mají stejnou vzdálenost od A jako od B.

Osa strany AB v rovině ρ jako množina bodů:

{X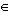ρ; |AX| = |BX|}

Pro dvě osy existuje jeden průsečík, pro který platí, že je stejně vzdálený od všech tří vrcholů, tedy jím musí procházet i osa třetí.

Kružnice opsaná

Protože je průsečík os stran stejně vzdálen od všech tří vrcholů trojúhelníku, můžeme zkonstruovat kružnici, která bude vrcholy procházet. Taková kružnice má střed S_o, poloměr |S_oA| a nazývá se opsaná, značíme k_o. Konstrukce kružnice opsané je podrobně rozveden v příkladu 1 kružnic.