Příklad 1
Mějme různé body A, B. Odvoďte a narýsujte množinu M bodů dané vlastnosti.
M = {X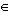  ρ; |AX| = |AB| + |BX|}
ŘEŠENÍ

Příklad 2
Mějme různé body A, B. Odvoďte a narýsujte množinu M bodů dané vlastnosti.
M = {X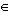  ρ; |AX|² = |AB|² + |BX|²}
ŘEŠENÍ

Příklad 3
Mějme různé body A, B. Odvoďte a narýsujte množinu M bodů dané vlastnosti.
M = {X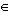  ρ; |AB|² = |AX|² + |BX|²}
ŘEŠENÍ

Příklad 4
Mějme přímku p a bod A; A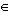  p. Odvoďte a narýsujte množinu M středů všech kružnic, které se přímky p dotýkají v bodě A.
ŘEŠENÍ

Příklad 5
Mějme různé body P, Q. Odvoďte a narýsujte množinu M všech bodů X takových, že PQX je rovnoramenný trojúhelník se základnou QX.
ŘEŠENÍ