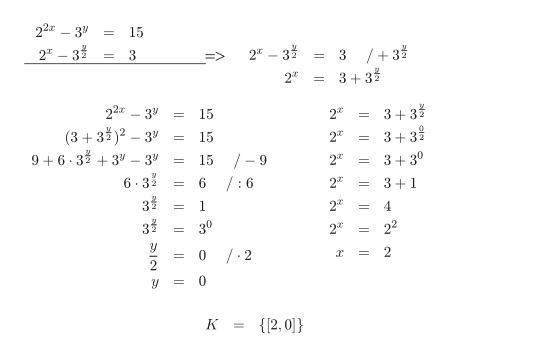Soustavy exponenciálních rovnic
Při řešení soustav exponenciálních rovnic nemusíme většinou určovat podmínky řešitelnosti. Zpravidla jsou rovnice definovány pro všechna reálná čísla. Řešení takových soustav rovnic ukážeme na následujících příkladech.
Řešte soustavu rovnic s neznámými x,y \in R:
- Výrazy v rovnici jsou definovány pro všechna x,y \in R.
- Z druhé rovnice 2^x=0,4y vyjádříme neznámou y:
y=\frac{5}{2}\cdot 2^x. - Do první rovnice 4^x=1,6y dosadíme za neznámou y výraz \frac{5}{2}\cdot 2^x:
4^x=1,6\cdot \frac{5}{2}\cdot 2^x . - Z předchozí rovnice určíme neznámou x (viz řešení exponenciálních rovnic):
x=2. - Neznámou y určíme z rovnice y=\frac{5}{2}\cdot 2^x dosazením x=2:
y=10 - Množina kořenů soustavy rovnic K=\{[2,10]\}.
Zápis řešení:

Řešte soustavu rovnic s neznámými x,y \in R:
- Výrazy v rovnici jsou definovány pro všechna x,y \in R.
- Z druhé rovnice 2^x-3^\frac{y}{2}=3 vyjádříme výraz 2^x, který v následujícím kroku snadno dosadíme do první rovnice:
2^x=3+3^{\frac{y}{2}}. - Do první rovnice 2^{2x}-3^y=15 dosadíme za výraz 2^x výraz 3+3^{\frac{y}{2}}:
(3+3^\frac{y}{2})^2-3^y=15. - Z předchozí rovnice určíme neznámou y (viz řešení exponenciálních rovnic):
y=0. - Neznámou x určíme z rovnice 2^x=3+3^{\frac{y}{2}} dosazením y=0 (řešení exponenciální rovnice):
x=2 - Množina kořenů soustavy rovnic K=\{[2,0]\}.
Zápis řešení: