Grafické řešení exponenciálních rovnic
U exponenciálních rovnic nemáme žádný univerzální algoritmus, pomocí kterého bychom určili řešení každé exponenciální rovnice. Některé exponenciální rovnice jsme se naučili řešit v předchozích kapitolách. Další rovnice můžeme řešit přibližně pomocí numerických metod a počítačů. V této kapitole ukážeme, jak přibližně řešit takové exponenciální rovnice za pomoci grafu funkce.
Často lze při řešení rovnic využít grafy funkcí. Připomeneme, jak lze graficky řešit lineární rovnici 2x+4=-x+1. Výraz na levé straně rovnice si představíme jako předpis funkce y=2x+4 a výraz na pravé straně rovnice jako předpis funkce
y=-x+1. Řešením této rovnice je x-ová souřadnice průsečíků grafů těchto funkcí.
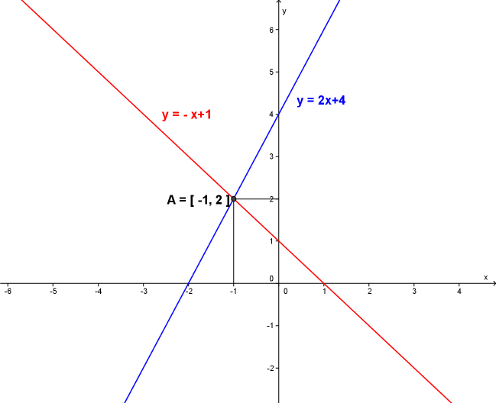
Grafy funkcí y=2x+4 a y=-x+1 vidíte na obrázku. Průsečíkem grafů je bod A=[-1,2]. Řešením rovnice 2x+4=-x+1 je tedy číslo x=-1.
Jindy je výhodnější, když všechny výrazy v rovnici převedeme na levou stranu rovnice a na pravé straně rovnice nám zbyde pouze 0. Řešením takové rovnice jsou potom
x-ové souřadnice průsečíků grafu funkce s osou x, protože grafem funkce y=0 je přímka totožná s osou x.
Ukážeme, jak graficky vyřešit rovnici x^2=5x-6. Převedeme všechny výrazy na levou stranu rovnice a získáme rovnici x^2-5x+6=0. Nakreslíme graf funkce
y=x^2-5x+6 a najdeme jeho průsečíky s osou x.
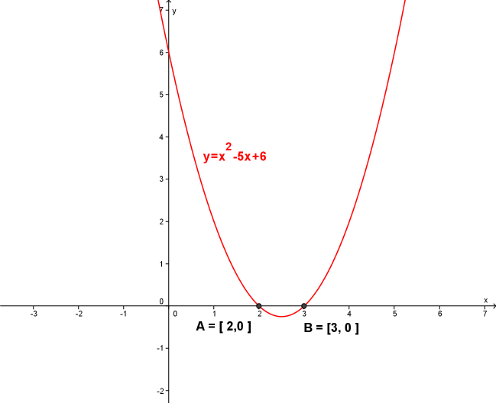
Graf funkce y=x^2-5x+6 vidíte na obrázku. Protíná osu x v bodech
A=[2,0] a B=[3,0]. Řešením rovnice x^2=5x-6 jsou tedy čísla
x_1=2, x_2=3.
Ke grafickému řešení rovnice využijeme program, který umí vykreslit graf funkce a zjistit jeho průsečíky s osou x. K takovým programům patří GEOGEBRA.
Na těchto stránkách je vystaven Java applet, pomocí kterého můžeme řešit exponenciální rovnice, aniž bychom museli mít tento program nainstalovaný. Přesný popis ovládání Java appletu nyní představíme. Samotný applet najdete na konci této kapitoly.
Java applet, který máme k dispozici, lze použít k mnoha účelům (např. k dynamickým konstrukcím). My ukážeme jeho využití při řešení rovnic. Všechny důležité prvky, které budeme potřebovat, jsou vyznačeny na následujícím obrázku a jsou očíslovány dle pořadí, ve kterém je budeme využívat.
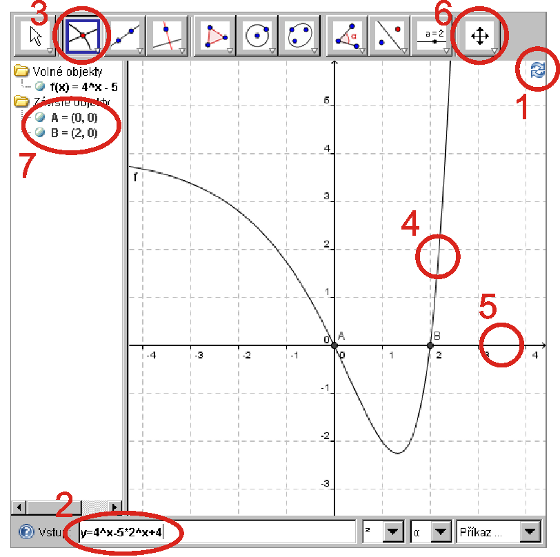
Nyní popíšeme jednotlivé prvky, které jsme zvýraznili v předchozím obrázku.
- Tlačítko k obnovení appletu.
- Vstupní pole pro předpis funkce.
- Nástroj k určení průsečíku.
- Graf funkce - první objekt k určení průsečíku.
- Osa x - druhý objekt k určení průsečíku.
- Nástroje pro posunutí, přiblížení a oddálení.
- Souřadnice průsečíků.
Zbývá ukázat, jak z klávesnice zadat předpis funkce (bod 2 v našem postupu). Do příkazové řádky napíšeme " y= " a následuje výraz s jedinou neznámou x. Pravidla při psaní výrazů jsou shrnuty v následující tabulce.
| Operace | Matematický zápis | Vstup appletu |
|---|---|---|
| Aritmetické operace | +,-,\cdot,: | +,-,*,/ |
| Obecná mocnina | a^b | a^(b) |
| Obecná odmocnina | \sqrt[b]{a} | a^(1/b) |
| Absolutní hodnota | |x| | abs(x) |
| Goniometrické funkce | sin x, cos x tg x, cotg x |
sin(x), cos(x) tan(x), 1/(tan(x)) |
Místo desetinné čárky je nutné psát tečku!
Je lepší psát * pro každou operaci násobení, přestože jí často v matematickém zápisu vynecháváme!
Na závěr této části uvedeme, jak bychom zadali předpisy některých funkcí do Java appletu.
| Matematický zápis | Vstup appletu |
|---|---|
| y=x^2-4x+5 | y=x^2-4*x+5 |
| y=\sqrt{x+3}+1 | y=(x+3)^(1/2)+1 |
| y=||x-1|-2|-3 | y=abs(abs(x-1)-2)-3 |
| y=3^{x+2}-27 | y=3^(x+2)-27 |
| y=2^{x^2-3x+1}-5 | y=2^(x^2-3*x+1)-5 |
Následující applet nám bude sloužit ke grafickému řešení exponenciálních rovnic.
4^x-5\cdot 2^x+4=0
- Budeme postupovat přesně dle instrukcí, popsaných v předchozí části.
- Do vstupního pole zadáme předpis funkce y=4^x-5*2^x+4 .
- Najdeme průsečíky grafu funkce s osou x.
- Jsou jím body [0,0], [2,0].
- Řešením této rovnice jsou tedy x-ové souřadnice těchto bodů.
- K=\{0,2\}
Tento příklad byl použit při popisu ovládání appletu. Jeho řešení tedy odpovídá tomuto obrázku.
Tuto rovnici jsme již řešili v příkladu 4.11 pomocí substituce a můžeme ověřit, že jejím řešením jsou stejná čísla.
Řešte graficky s využitím appletu rovnice s neznámou x\in R:
| 2^x+3^x=4^x | 2^{x^2-5}=x^2-1 |
2^x+3^x-4^x=0 |
2^{x^2-5}-x^2+1=0 |
y=2^x+3^x-4^x |
y=2^(x^2-5)-x^2+1 |
 |
 |
K=\{1,51\} |
K=\{\pm1,03;\pm2,78\} |
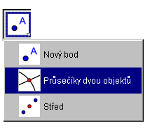 Tento nástroj slouží k určení průsečíku. Pokud nemáte tento násroj v nabídce, zvolte ho pomocí rozbalovacího menu. Potom klikněte na ikonu s průsečíkem. Než přistoupíte k bodům 4 a 5 je nutné mít tento nástroj aktivní. To poznáte tak, že okolo tohoto nástoje je modrý rámeček.
Tento nástroj slouží k určení průsečíku. Pokud nemáte tento násroj v nabídce, zvolte ho pomocí rozbalovacího menu. Potom klikněte na ikonu s průsečíkem. Než přistoupíte k bodům 4 a 5 je nutné mít tento nástroj aktivní. To poznáte tak, že okolo tohoto nástoje je modrý rámeček.  V bodě 4 a 5 jste určili jeden z průsečíků grafu s osou
V bodě 4 a 5 jste určili jeden z průsečíků grafu s osou