Aplikace logaritmických vět
Nebudeme nyní zavádět žádné další ekvivalentní úpravy. Stejně jako v předchozí kapitole budeme rovnice řešit porovnáním argumentů. V jednotlivých odstavcích ukážeme, jak lze upravit výrazy v logaritmické rovnici, aby ji bylo možné řešit porovnáním argumentů.
Logaritmické rovnice budeme upravovat pomocí vět o logaritmech, které souhrnně připomeneme v následujícím rámečku. Tentokrát v argumentech logaritmu nebudou jen čísla, ale výrazy s neznámou, které symbolicky zapisujeme f(x), g(x).
\log_a f(x)-\log_a g(x)=\log_a \frac{f(x)}{g(x)}
g(x)\log_a f(x)=\log_a f(x)^{g(x)}
Nejprve ukážeme, jak řešíme rovnice, kde se vyskytuje součet a rozdíl několika logaritmů, které mají stejný základ. V těchto příkladech využíváme poučku, že součet logaritmů je logaritmus součinu a rozdíl logaritmů je logaritmus podílu za předpokladu, že všechny výrazy jsou definovány.
- a) \log_3(x+7)-\log_3 2x=\log_3 4
- b) \log_2(x+1)+\log_2(x-1)-3=\log_2(x-2)
- a)
- Výrazy v rovnici jsou definovány, pokud jsou splněny podmínky x+7>0 a 2x>0.
- Definiční obor rovnice D=(0,+\infty).
- Výraz na levé straně rovnice obsahuje rozdíl dvou logaritmů se stejným základem. Rozdíl logaritmů je logaritmus podílu:
L(x)=\log_3(x+7)-\log_3 2x=\log_3 \frac{x+7}{2x}. - Rovnici \log_3 \frac{x+7}{2x}=\log_3 4 vyřešíme porovnáním argumentů.
- Získáme ekvivalentní rovnici \frac{x+7}{2x}=4, jejímž řešením je x=1.
- Číslo 1 leží v definičním oboru rovnice, proto K=\{1\}.
Zápis řešení:

- b)
- Výrazy v rovnici jsou definovány, pokud jsou splněny podmínky x+1>0,
x-1>0 a x-2>0. - Definiční obor rovnice D=(2,+\infty).
- Výraz na levé straně rovnice obsahuje kromě logaritmů i číslo 3. Abychom mohli použít věty o logaritmech, musíme nejprve převést číslo 3 na logaritmus o základu 2:
3=\log_2 8. - Na levou stranu rovnice aplikujeme věty o logaritmech součtu a rozdílu:
L(x)=\log_2(x+1)+\log_2(x-1)-\log_2 8=\log_2\frac{(x+1)(x-1)}{8}. - Rovnici \log_2\frac{(x+1)(x-1)}{8}=\log_2(x-2) vyřešíme porovnáním argumentů.
- Získáme ekvivalentní rovnici \frac{(x+1)(x-1)}{8}=x-2, která po úpravě vede na kvadratickou
rovnici, jejímž řešením jsou čísla x_1=3 a x_2=5. - Číslo 3 i 5 leží v definičním oboru rovnice, proto K=\{3,5\}.
Zápis řešení:
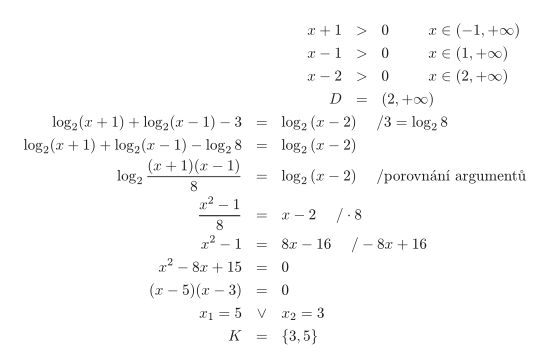
| \log_5 x + \log_5(x-3)=\log_5 4 | \log_3(4y+1)-2=\log_3(y-1) |
D=(3,+\infty) |
D=(1,+\infty) |
\log_5 x(x-3)=\log_5 4 |
\log_3(4y+1)-\log_3 9=\log_3(y-1) |
x(x-3)= 4 |
\log_3\frac{4y+1}{9}=\log_3(y-1) |
x^2-3x-4= 0 |
\frac{4y+1}{9}=(y-1) |
(x-4)(x+1)= 0 |
4y+1=9y-9 |
x_1=4~~~x_2=-1 |
10=5y |
4\in D,~~-1\notin D |
y=2 |
K=\{4\} |
2\in D |
K=\{2\} |
Další věta o logaritmech nám umožňuje převést násobek před logaritmem do argumentu logaritmu. V kapitole o logaritmických větách jsme zjednodušeně říkali, že násobek logaritmu je logaritmus mocniny.
- Výrazy v rovnici jsou definovány, pokud jsou splněny podmínky
6x-2>0 a x-3>0. - Definiční obor rovnice D=(3,+\infty).
- Logaritmus na pravé straně rovnice je vynásoben číslem 2. Převedeme toto číslo do argumentu logaritmu:
P(x)=2\log_8(x-3)=\log_8(x-3)^2. - Rovnici \log_8(6x-2)=\log_8(x-3)^2 vyřešíme porovnáním argumentů.
- Získáme ekvivalentní rovnici 6x-2=(x-3)^2, která po úpravě vede na kvadratickou rovnici, jejímž řešením jsou čísla x_1=1 a x_2=11.
- Číslo 11 leží v definičním oboru rovnice, ale číslo 1 neleží v definičním oboru rovnice, proto K=\{11\}.
Zápis řešení:

- Výrazy v rovnici jsou definovány, pokud jsou splněny podmínky
x+1>0, x+4>0 a x>0. - Definiční obor rovnice D=(0,+\infty).
- Na levé straně rovnice upravíme výraz pomocí vět o logaritmech:
L(x)=2\log(x+1)=\log(x+1)^2. - Na pravé straně rovnice také upravíme výraz pomocí vět o logaritmech:
P(x)=\log(x+4)+\log x=\log x(x+4). - Rovnici \log(x+1)^2=\log x(x+4) vyřešíme porovnáním argumentů.
- Získáme ekvivalentní rovnici (x+1)^2=x(x+4), která po úpravě vede na lineární rovnici, jejímž řešením je x=\frac{1}{2}.
- Číslo \frac{1}{2} leží v definičním oboru rovnice, proto K=\{\frac{1}{2}\}.
Zápis řešení:
