Grafické řešení logaritmických rovnic
Na konci kapitoly o exponenciálních rovnicích jsme se naučili řešit exponenciální rovnice, které nešly řešit žádnou nám známou metodou. Nyní se naučíme řešit logaritmické rovnice, které nelze řešit žádnou metodu zmiňovanou v předchozích kapitolách. Půjde o grafické řešení logaritmických rovnic.
Nejprve shrneme, co jsme se naučili v kapitole Grafické řešení exponenciálních rovnic:
- Řešením rovnice f(x)=0 jsou x-ové souřadnice průsečíků grafu funkce
y=f(x) s osou x. - Ke grafickému řešení rovnic využijeme program GEOGEBRA, který umí vykreslit graf funkce a určit jeho průsečíky s osou x.
- Naučili jsme se ovládat Java applet.
- Naučili jsme se zadat předpis funkce do Java appletu.
Zbývá nám tedy ukázat, jak zadat předpis logaritmické funkce do Java appletu. Do programu GEOGEBRA lze zadat pouze funkce přirozený a dekadický logaritmus. Logaritmy dalších základů zadáváme jako podíl dvou logaritmů.
| Operace | Matematický zápis | Vstup appletu |
|---|---|---|
| Dekadický logaritmus | \log x | lg(x) |
| Přirozený logaritmus | \ln x | ln(x) |
| Obecný logaritmus | \log_a x | lg(x)/lg(a) |
Ještě si ukážeme, jak lze zadat předpisy funkcí s logaritmy do Java appletu:
| Matematický zápis | Vstup appletu |
|---|---|
| y=\log_5(x+3) | y=lg(x + 3) / lg(5) |
| y=\log_{x+1}2 | y= lg(2) / lg(x + 1) |
| y=\log^25x-\log5x | y=(lg(5 x))² - lg(5 x) |
| y=\log_5 \frac{x^2+1}{x-1}-1 | y=lg((x² + 1) / (x - 1)) / lg(5) - 1 |
Pomocí následujícího appletu budeme graficky řešit logaritmické rovnice.
Využití appletu si ukážeme na jednoduchém příkladu.
\log_\frac{1}{2}(2-x)=-2
- Budeme postupovat přesně dle instrukcí, popsaných v kapitole o grafickém řešení exponenciálních rovnic.
- Převedeme všechny výrazy v rovnici na levou stranu:
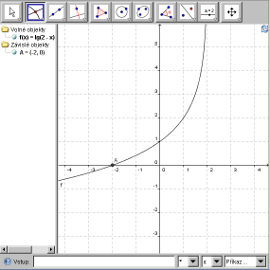
\log_\frac{1}{2}(2-x)+2=0. - Do vstupního pole zadáme předpis funkce y=lg(2-x)/lg(1/2)+2 .
- Najdeme průsečíky grafu funkce s osou x.
- Je jím bod [-2,0].
- Řešením této rovnice je tedy x-ová souřadnice tohoto bodu.
- K=\{-2\}.
Tuto rovnici jsme již řešili v příkladu 5.4 porovnáním argumentů. Vidíme, že jsme jinou metodou dosáhli stejného výsledku.
Řešte graficky s využitím appletu rovnice s neznámou x\in R:
| \log_2 x^2=x-1 | \log_7 |x|= \sin x |
\log_2 x^2-x+1=0 |
\log_7 |x|- \sin x=0 |
y=lg(x^2)/lg(2)-x+1 |
y=lg(abs(x))/lg(7)-sin(x) |
 |
 |
K=\{-0,58;1;6,23\} |
K=\{-5,26;-3,92;-0,44;2,62\} |