Exponenciální funkce

Zavedení a graf exponenciální funkce

V kapitole o mocninách jsem vysvětlili, čemu říkáme exponent. Nyní zavedeme exponenciální funkci. Exponenciální funkce je taková funkce, v jejímž předpisu je proměnná x v exponentu.

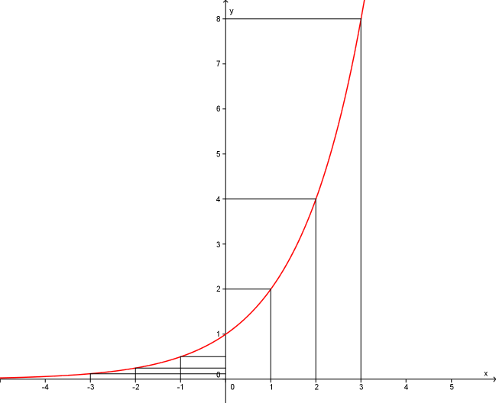
Exponenciální funkce o základu a \in R^+ - \{1\} je každá funkce na množině R zapsaná ve tvaru
y=a^x.

Nyní známe předpis exponenciální funkce. Zkusíme vypočítat několik funkčních hodnot a získat tak graf exponenciální funkce y=2^x. Zkuste samostatně doplnit tabulku:

x -3 -2 -1 0 1 2 3 4
y=2^x
0,125
0,25
0,5
1
2
4
8
16

Nakreslíme graf této funkce:

NAHORU
Vliv základu na graf exponenciální funkce

V následujícím appletu měňte velikost základu a pozorujte, jak se mění graf exponenciální funkce (klikněte levým tlačítkem na červené kolečko a tažením myši změníte hodnotu základu a).

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Na základě pozorování appletu doplňte:

NAHORU
Vlastnosti exponenciální funkce
Exponenciální funkce f: y=a^x, a>0, a\neq 1
Definiční obor D(f)=R
Obor hodnot H(f)=(0,+\infty)
Rostoucí pro a>1
Klesající pro a \in (0,1)
Prostá pro všechny přípustné základy
NAHORU
Porovnání mocnin

Následující applet nám bude sloužit k porovnávání dvou mocnin o stejném kladném základu.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com
Poznámka

Použití appletu si ukážeme na jednoduchém příkladu.

Příklad 3.5
Rozhodněte, která z mocnin je větší:

2^1~?~2^2

Řešení
    Využijeme applet:
  • Na modrém posuvníku nastavíme hodnotu základu a=2.
  • Na červeném posuvníku nastavíme velikost prvního exponentu x_1=1.
    První mocnina y_1=2^1=2.
  • Na zeleném posuvníku nastavíme velikost druhého exponentu x_2=2.
    Druhá mocnina y_2=2^2=4.
  • Z grafu je vidět, že y_1 < y_2, proto 2^1<2^2.
Zápis řešení:

2^1~?~2^2 \rightarrow 2^1=2, 2^2=4, proto 2^1<2^2

Cvičení 3.5
Rozhodněte, která z mocnin je větší:
0,5^{-1,5}~?~0,5^{2}
0,5^{-1,5}=2,83
0,5^{2}=0,25
0,5^{-1,5}>0,5^{2}
1,2^{4}~?~1,2^{-2}
1,2^{4}=2,07
1,2^{-2}=0,69
1,2^{4}>1,2^{-2}
3^{0,4}~?~3^{0,8}
3^{0,4}=1,55
3^{0,8}=2,41
3^{0,4}<3^{0,8}
(\frac{1}{5})^{\frac{1}{2}}~?~(\frac{1}{5})^{\frac{1}{5}}
0,2^{0,5}=0,45
0,2^{0,2}=0,72
(\frac{1}{5})^{\frac{1}{2}}<(\frac{1}{5})^{\frac{1}{5}}

Při řešení předchozího cvičení jsme si mohli všimnot následujících zákonitostí při porovnání dvou mocnin se stejným základem (jde o porovnání argumentů rostoucí a klesající funkce, které jsme vysvětlili v předchozí kapitole).

    Je-li základ mocniny
  • a \in (0,1), potom když je
    • první exponent menší než druhý, je první mocnina větší než druhá.
    • první exponent větší než druhý, je první mocnina menší než druhá.
  • a >1, potom když je
    • první exponent menší než druhý, je první mocnina menší než druhá.
    • první exponent větší než druhý, je první mocnina větší než druhá.
NAHORU