Využití logaritmů v praxi
V této kapitole představíme několik praktických aplikací logaritmů. Nejprve ukážeme, jak se pomocí logaritmů počítaly složité výpočty v době, kdy lidé něměli k dispozici kalkulačky, a zároveň vysvětlíme, jaký obrázek se nachází v hlavičce těchto stránek. Nakonec ukážeme výhodu použití logaritmické stupnice, která se používá dodnes.
Ve škole v matematice často počítáme příklady, které obsahují pouze "jednoduchá" čísla (stejně jako v této práci). V praxi naopak pracujeme s čísly "ošklivými", která získáváme například fyzikálním měřením nebo z popisu reálné situace. Taková čísla obsahují větší počet cifer a je obtížné s nimi provádět základní matematické operace jako násobení, dělení, umocňování či odmocňování. V tomto odstavci ukážeme, jak s takovými čísly počítat bez použití kalkulačky.
Naším cílem tedy bude převést "složité" početní operace na nějaké "jednodušší", které budou pro počítání přijatelnější. Začněme s násobením velkých čísel a postupně ukážeme, jak podobným postupem zjednodušit ostatní operace. Předpokládejme, že chceme určit součin 147,153\cdot 45~967,2.
Nikomu z nás se nejspíš nebude chtít zapsat si tato dvě čísla pod sebe a vynásobit pomocí algoritmu, který jsme se naučili na základní škole. Pokud bychom však měli tato dvě čísla sečíst, nedělalo by nám to zas tak velké problémy. Sčítání je určitě jednodušší operace než násobení. Převádět součin na součet jsme se již ale naučili v předchozí kapitole, tedy za předpokladu, že součin byl v argumentu logaritmu. Zjistili jsme, že logaritmus součinu je součet logaritmů.
Už víme, že kdybychom uvedený součin měli v argumentu logaritmu, mohli bychom místo násobení sčítat. Vyjádřit číslo pomocí logaritmu však umíme. Využijeme vztah mezi mocinou a logaritmem z předchozí kapitoly: 10^{\log {r}}=r. Proč je vhodné zvolit za základ mocniny i logaritmu číslo 10, vysvětlíme později.
To znamená, že součin 147,153\cdot 45~967,2 lze převést na
10^{\log 147,153\cdot 45~967,2}=10^{\log 147,153+\log 45~967,2}.
Výpočet příkladu můžeme shrnout ve třech bodech (předpokládejme, že umíme bez kalkulačky určit dekadický logaritmus a mocninu libovolného čísla):
- Určíme dekadické logarimy obou čísel: \log 147,153\doteq2,167~8 ;~ \log 45~967,2\doteq4,662~4.
- Logaritmy sečteme: 2,167~8+4,662~4=6,830~2.
- Vypočítáme mocninu s tímto exponentem: 10^{6,830~2}\doteq6~763~943,948.
Pokud využijeme další logaritmické věty, můžeme snadno vypočítat podíl, mocninu nebo odmocninu velkých čísel pomocí vztahů:
a\cdot b=10^{\log a \cdot b}=10^{\log a+\log b},
a:b=10^{\log a : b}=10^{\log a-\log b},
a^b=10^{\log a^b}=10^{b\cdot \log a},
\sqrt[b]{a}=a^{\frac{1}{b}}=10^{\log a^{\frac{1}{b}}}=10^{\frac{1}{b}\cdot \log a}.
- Doposud jsme neobjasnili následující:
- Jak určit dekadické logaritmy a mocninu bez kalkulačky.
- Proč jsme zvolili právě logaritmus a mocninu o základu 10.
Zatím umíme logaritmus a mocninu vypočítat na kalkulačce. Na začátku této kapitoly jsme ale předpokládali, že kalkulačku nemáme k dispozici. Ukážeme, že dekadické logaritmy i mocniny lze také určit pomocí logaritmického pravítka nebo z logaritmických tabulek.
Logaritmické pravítko je matematická pomůcka používaná v minulém století k přibližnému určování zejména technických výpočtů. Mimo jiné umožňuje určit přibližnou hodnotu dekadického logaritmu s argumentem z intervalu <1,10) a naopak určit mocninu se základem 10 a s exponentem z intervalu <0,1).

Logaritmické tabulky jsou určeny k přesným technickým výpočtům. Umožňují určit dekadické logaritmy s argumentem z intervalu <1,10) s přesností až na 10 platných cifer (nebo obráceným způsobem mocninu). Část logaritmických tabulek je znázorněna na následujícím obrázku. Tato část tabulky umožňuje určit logaritmy čísel z intervalu 1,069 až 1,069 12 (pokud by byly k dispozici i zbylé sloupce).
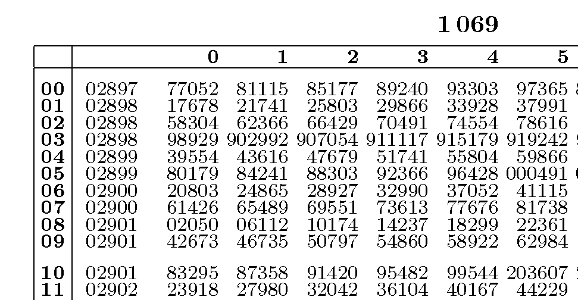
Logaritmické pravítko i logaritmické tabulky umožnily určit dekadické logaritmy s argumentem pouze z intervalu <1,10). Abychom určili logaritmus libovolného čísla, využijeme jeho semilogaritmický (nebo též vědecký) zápis ve tvaru x\cdot 10^y, kde
x\in <1,10) a y\in Z.
Logaritmus takového čísla určíme snadno:
\log x\cdot 10^y=\log x +\log 10^y=\log x + y.
Určit exponent y jsme se učili na základní škole a \log x určíme pomocí logaritmického pravítka nebo tabulek.
V matematice a ve fyzice jsme zvyklí závislosti zakreslovat grafem v soustavě souřadnic. Pokud jedna z proměnných roste mnohem rychleji než druhá proměnná, zvolíme místo lineární stupnice stupnici logaritmickou (např. místo hodnot 1, 10, 100, 1000 budeme na osu vynášet dekadické logaritmy těchto hodnot 0, 1, 2, 3). Pro takové grafy s výhodou využijeme lagaritmický papír s logaritmickou stupnicí na ose x.
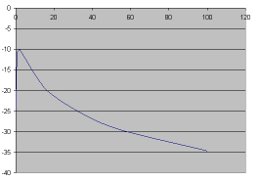
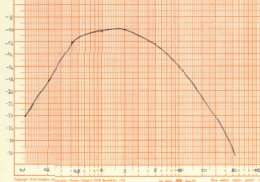
Nakonec ukážeme, jak vypadá graf (charakteristika) jedné elektronické součástky (Wienův článek) zakreslený v prvním případě v lineární soustavě souřadnic (graf vlevo) a v druhém případě v logaritmickém měřítku (graf vpravo). Porovnáním obou grafů můžeme snadno rozhodnout, že pravý graf v logaritmickém měřítku lépe vystihuje funkci této součástky.
Decibel (zkratka dB) je jednotka, kterou možná znáte jako jednotku hladiny intenzity zvuku, ale můžete se s ní sektat i v elektronice a dalších oborech. Ve skutečnosti jde o podíl dvou hodnot, který je zlogaritmován (decibel lze chápat podobně jako např. procento, které také udává podíl dvou hodnot).
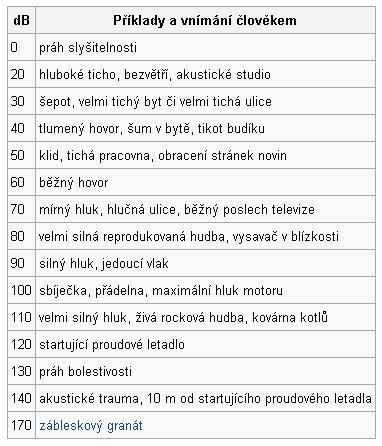
Vědci dokázali, že lidský organismus nevnímá podněty (zvuk, světlo) lineárně s jejich intenzitou, ale naopak logaritmicky. Proto je například u měření hladiny intenzity zvuku použito logaritmické měřítko a jednotka decibel. Platí, že zvýšení o 3 dB odpovídá přibližně dvojnásobné intenzitě podnětu. Protože se jedná o logaritmickou závislost, zvýšení o 30 dB odpovídá již přibližně tisíckrát zvětšené intenzitě podnětu.
Jednotka decibel se využívá také v elektronice. Zejména při popisu útlumu a zisku signálu. Zde je výhoda použití decibelu hned dvojí. Nejen, že výsledné hodnoty se lépe vyjadřují v logaritmickém měřítku, ale zároveň se s touto jednotkou lépe pracuje. Zisk i útlum se totiž počítají jako podíl výstupního ku vstupnímu výkonu elektronické součástky. Pokud bychom nepoužili decibel, museli bychom dva útlumy nebo zisky mezi sebou násobit. Díky jednotce decibel se však násobení, vzhledem k vlastnostem logaritmů, převádí na sčítání.
Abychom ukázali využití decibelů v praxi, uvažujme následující situaci. Na střeše máme anténu, která nám zajišťuje připojení na internet. Z antény nám vede 12 m dlouhý kabel do počítače, který je v jednom místě spojen oboustrannou spojkou. Z technické dokumentace víme, že anténa má zisk 9 dB, kabel má útmul 0,2 dB/m a spojka má útlum 3 dB. Úkolem je vypočítat celkový zisk signálu.
Celkový zisk signálu se počítá jako součet všech zisků v přenosové soustavě. Útlum signálu snadno převedeme na zisk záměnou znaménka (má-li spojka útlum 3 dB je její zisk -3 dB).
- Zisk antény je 9 dB.
- Celkový útlum kabelu je 12\cdot 0,2=2,4~dB, což odpovídá zisku -2,4 dB.
- Zisk spojky je -3 dB.
- Celkový zisk signálu je 9-2,4-3=3,6~dB.