Logaritmická nerovnice

Na logaritmické nerovnice lze opět nahlížet i jinak. Logaritmická nerovnice vznikne z logaritmické rovnice nahrazením symbolu rovnosti = jedním ze symbolů nerovnosti <, >, \leq, \geq.

Co znamená vyřešit nerovnici jsme již připomněli v kapitole o exponenciálních nerovnicích.

Postup při řešení nerovnice jsme již vysvětlili v kapitole o exponenciálních nerovnicích. Na rozdíl od exponenciálních nerovnic je potřeba si dávat pozor na určování definičního oboru logaritmické nerovnice.

Postup při určování definčního oboru logaritmické nerovnice je stejný, jako určování definičního oboru logaritmických rovnic. Připomeňme si, že do definičního oboru logaritmické nerovnice patří čísla, pro která je:

• argument logaritmu větší než nula,
• základ logaritmu větší než nula a různý od jedné.

Zbývá ukázat, jak určíme množinu všech kořenů K. Předpokládejme, že chceme určit řešení nerovnice, jejíž definiční obor D=(3,8) a úpravami původní nerovnice vznikne nerovnice x\geq 5.

Dohodneme se na následujícím postupu:
• Na číselné ose vyznačíme definiční obor nerovnice D=(3,8). Pro přehlednost ho zakreslíme modrou barvou.
• Následně na číselnou osu zakreslíme hodnoty, pro které je splněna nerovnost x\geq 5. Jedná se o interval <5,+\infty). Pro přehlednost ho zakreslíme černou barvou.
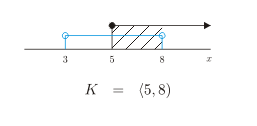
• Určíme průnik těchto intervalů, které na číslené ose vyznačíme šrafováním. Je jím interval <5,8).
• Hodnoty neznámých z tohoto intervalu jsou řešením původní nerovnice, proto množina všech kořenů K=<5,8).