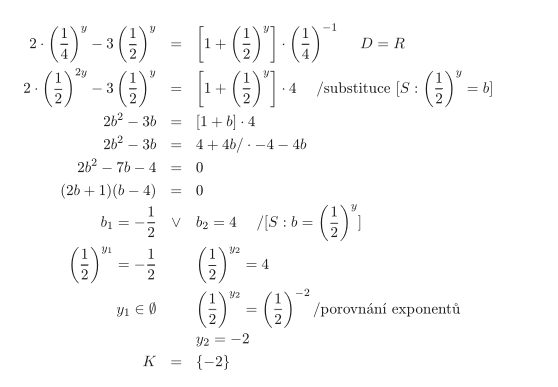Substituce
Při řešení rovnic jsme se již setkali s tzv. substitucí (např. při řešení bikvadratické rovnice).
- Nahradili jsme některý výraz v rovnici novou neznámou.
- Rovnici s novou neznámou jsme vyřešili.
- Řešení původní rovnice jsme získali prostřednictvím použité substituce.
Tuto úpravu budeme značit: [ S: V(x)=a ]
Při řešení rovnic používáme substituci dvakrát. Nejprve nahradíme výraz V(x) novou neznámou a. Tuto úpravu značíme [ S: V(x)=a ]. Po vyřešení rovnice s neznámou a, zpětně použijeme stejnou substituci. Tentokrát nahradíme neznámou a výrazem V(x), abychom získali řešení původní rovnice. Tuto zpětnou substituci budeme v řešených příkladech značit [ S: a=V(x) ].
Použití substituce nejlépe ukážeme na příkladech.
- a) 4^x-5\cdot 2^x+4=0
- b) 5^y+2=\frac{3}{5^y}
- c) 3^z+3^{1-z}=4
- a)
- Definiční obor rovnice D=R.
- Abychom mohli zavést substituci, musíme mocninu 4^x upravit: 4^x=(2^x)^2.
- V rovnici (2^x)^2-5\cdot 2^x+4=0 nahradíme všechny výrazy 2^x novou neznámou a.
- Rovnici a^2-5a+4=0 s neznámou a \in R vyřešíme.
- Řešením rovnice jsou čísla a_1=4, a_2=1.
- Zpětně nahradíme neznámou a výrazem 2^x, tj. a_1=2^{x_1}, a_2=2^{x_2}.
- Rovnice 2^{x_1}=4, 2^{x_2}=1 vyřešíme porovnáním exponentů.
- Řešením jsou čísla x_1=2, x_2=0 .
- Množina všech kořenů K=\{0,2\}.
Zápis řešení:

- b)
- Definiční obor rovnice D=R.
- V rovnici 5^y+2=\frac{3}{5^y} nahradíme všechny výrazy 5^y novou neznámou b.
- Získanou rovnici b+2=\frac{3}{b} s neznámou b \in R vyřešíme.
- Navíc můžeme celou rovnici násobit neznámou b, neboť víme, že není nikdy nulová.
Výraz 5^y je totiž vždy kladný. - Řešením rovnice jsou čísla b_1=-3, b_2=1.
- Zpětně nahradíme neznámou b výrazem 5^y.
- Získáme rovnice 5^{y_1}=-3, 5^{y_2}=1 .
- První rovnice 5^{y_1}=-3 nemá řešení. Mocnina s kladným základem je vždy kladná, proto se nemůže rovnat -3.
- Druhou rovnici 5^{y_2}=1 vyřešíme porovnáním exponentů: y_2=0
- Množina všech kořenů K=\{0\}.
Zápis řešení:

- c)
- Definiční obor rovnice D=R.
- Abychom mohli zavést substituci, musíme mocninu 3^{1-z} upravit:
3^{1-z}=3\cdot 3^{-z}=\frac{3}{3^z} - V rovnici 3^z+\frac{3}{3^z}=4 nahradíme všechny výrazy 3^z novou neznámou c.
- Rovnici c+\frac{3}{c}=4 s neznámou c \in R vyřešíme. Opět máme zajištěno, že c \neq 0 .
- Řešením jsou čísla c_1=3, c_2=1.
- Zpětně nahradíme neznámou c výrazem 3^z a získané rovnice řešíme porovnáním exponentů.
- Řešením jsou čísla z_1=1, z_2=0 .
- Množina všech kořenů K=\{0,1\}.
Zápis řešení:

| 9^x-80\cdot 3^x=81 | 6^{z+1}+6^{1-z}=37 |
D=R |
D=R |
(3^x)^2-80\cdot 3^x=81 |
6\cdot 6^z+\frac{6}{6^z}=37 |
a^2-80a=81 |
6a+\frac{6}{a}=37 |
a^2-80a-81=0 |
6a^2-37a + 6=0 |
(a-81)(a+1)=0 |
(a-6)(6a-1)=0 |
a_1=81,~~~a_2=-1 |
a_1=6,~~~a_2=\frac{1}{6} |
3^{x_1}=81,~~~3^{x_2}=-1 |
6^{z_1}=6,~~~6^{z_2}=\frac{1}{6} |
3^{x_1}=3^4,~~{x_2}\in\emptyset |
6^{z_1}=6^1,~~6^{z_2}=6^{-1} |
x_1=4 |
z_1=1,~~~z_2=-1 |
K=\{4\} |
K=\{-1,1\} |
Neexistuje univerzální návod, pomocí kterého bychom určili, jaký výraz máme nahradit novou neznámou. Záleží zejména na naší početní praxi a předvídavosti. V následujících příkladech ukážeme další rovnice, které lze řešit vhodnou substitucí. Než si projdete řešení, rozmyslete si, který výraz byste nahradili novou neznámou.
- Definiční obor rovnice D=R.
- Upravíme výraz 16^{0,5-x}, abychom mohli zavést substituci:
16^{0,5-x}=16^{-1\cdot(x-0,5)}=\frac{1}{16^{x-0,5}}. - Všechny výrazy 16^{x-0,5} nahradíme novou neznámou a.
- Rovnici a+\frac{1}{a}=\frac{17}{4} s neznámou a \in R vyřešíme.
- Řešením rovnice jsou čísla a_1=4, a_2=\frac{1}{4}.
- Zpětně nahradíme neznámou a výrazem 16^{x-0,5} a vzniklé rovnice vyřešíme porovnáním exponentů.
- Řešením jsou čísla x_1=1, x_2=0 .
- Množina všech kořenů K=\{0,1\}.
Zápis řešení:

- Definiční obor rovnice D=R.
- Upravíme výraz (\frac{1}{4})^y, abychom mohli zavést substituci: (\frac{1}{4})^y=(\frac{1}{2})^{2y}.
- Všechny výrazy (\frac{1}{2})^y nahradíme novou neznámou b.
- Rovnici 2b^2-3b=[1+b]\cdot4 s neznámou b \in R vyřešíme.
- Řešením rovnice jsou čísla b_1=-\frac{1}{2}, b_2=4.
- Zpětně nahradíme neznámou b výrazem (\frac{1}{2})^y a vzniklé rovnice vyřešíme porovnáním exponentů.
- První rovnice nemá řešení a řešením druhé rovnice je číslo y_2=-2 .
- Množina všech kořenů K=\{-2\}.
Zápis řešení: