Exponenciální nerovnice

Na exponenciální nerovnice lze nahlížet i jinak. Exponenciální nerovnice vznikne z exponenciální rovnice nahrazením symbolu rovnosti = jedním ze symbolů nerovnosti <, >, \leq, \geq.

Připomeneme si , co znamená vyřešit nerovnici.

Při řešení nerovnice mohou nastat různé případy při určování množiny všech kořenů. Často půjde o nekonečně mnoho čísel, které zapisujeme pomocí intervalu či jejich sjednocení. Např. nerovnici x <5 s neznámou x \in R vyhovují čísla z intervalu (-\infty,5). Množina všech kořenů této nerovnice je tedy K=(-\infty,5).

Postup při řešení nerovnic se bude skládat ze stejných kroků jako postup při řešení rovnic:

1. Určíme obor řešení nerovnice O.
2. Určíme definiční obor nerovnice D .
3. Řešíme nerovnici s využitím ekvivalentních úprav.
4. Určíme množinu všech kořenů nerovnice K.

Upozorníme na několik drobností, ve kterých se liší řešení rovnic a nerovnic.

Liší se ekvivalentí úpravy rovnic a nerovnic:

• Při násobení nerovnice záporným číslem otáčíme znak nerovnosti.
• Nesmíme násobit nerovnici výrazem, který může nabývat kladných i záporných hodnot (pokud si nejste jisti, vyvarujte se násobení výrazem s neznámou).
• Liší se použití ekvivalentních úprav zavedených v této práci (porovnání exponentů, logaritmování a porovnání argumentů). Jednotlivými úpravami se budeme zabývat v následujících kapitolách.

Ekvivalentními úpravami nerovnici upravíme na tvar, ze kterého můžeme určit řešení. Mezi takové jednoduché tvary patří:

• Nerovnice, které přímo dávají podmínku pro neznámou x, např. nerovnice x>2.
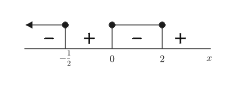
• Nerovnice v součinovém tvaru, např. nerovnice x(x-2)(2x+1)\leq 0. K řešení takové nerovnice použijeme číselnou osu, jak je vidět na obrázku.
• Kvadratické nerovnice, které převedeme na součinový tvar a řešíme jako v předchozím bodě. Např. nerovnici 2x^2+x-3>0 převedeme na nerovnici (2x+3)(x-1)>0, která je již v součinovém tvaru.

Zbývá určit množinu všech kořenů K. Do množiny všech kořenů patří takové hodnoty neznámé x získané v předchozím kroku, které leží v definičním oboru nerovnice. Pokud jsou definičním oborem všechna reálná čísla, potom je množina všech řešení K~ rovna řešení, získanému ekvivalentními úpravami nerovnice (typické pro exponenciální nerovnice a zcela výjimečné pro logaritmické nerovnice).