Porovnání argumentů

Základní úprava

Nejjednodušším typem logaritmické nerovnice je nerovnice ve tvaru \log_a {f(x)} < \log_a {g(x)} nebo nerovnice, které lze ekvivalentními úpravami převést na tento tvar. Řešení takové nerovnice využívá zákonitostí, které jsme odvodili při porovnávání dvou logaritmů.

Při řešení takové nerovnice musíme rozlišit dva případy.

Podrobně je porovnání argumentů rostoucí a klesající funkce vysvětleno v kapitole o funkcích.

Nerovnice \log_a {f(x)} < \log_a {g(x)} s neznámou x \in R je ekvivalentní s nerovnicí
  • f(x) < g(x), pro a > 1,
  • f(x) > g(x), pro a \in (0,1).
Tuto ekvivalentní úpravu budeme nazývat porovnání argumentů.

Zatím jsme zmínili pouze logaritmické nerovnice, kde byl použit znak nerovnosti <. Stejným způsobem se řeší i nerovnice, kde jsou použity znaky nerovnosti >, \leq, \geq. Při porovnání argumentů platí:

Porovnáváme-li argumenty logaritmů se základem a > 1,
neotáčíme znaménko nerovnosti.
Porovnáváme-li argumenty logaritmů se základem a \in (0,1),
otáčíme znaménko nerovnosti.
Příklad 7.1
Řešte nerovnice s neznámou x \in R:
  1. a) \log_2(2x+1)>\log_2(x+7)
  2. b) \log_\frac{1}{3}(x+5)\leq \log_\frac{1}{3}(5x-3)
Řešení
    a)
  • Výrazy v nerovnici jsou definovány, pokud jsou splněny podmínky
    2x+1>0 a x+7>0.
  • Definiční obor nerovnice D=(-\frac{1}{2},+\infty).
  • Porovnáme argumenty logaritmů na obou stranách nerovnice. Protože je základ logaritmu větší než jedna, neotáčíme znak nerovnosti.
  • Získáme nerovnici 2x+1>x+7, která je ekvivalentní s nerovnicí x > 6.
  • Na číselné ose určíme průnik definičního oboru a řešení předchozí nerovnice.
  • Množina všech kořenů původní nerovnice K=(6,+\infty).

Zápis řešení:

    b)
  • Výrazy v nerovnici jsou definovány, pokud jsou splněny podmínky
    x+5>0 a 5x-3>0.
  • Definiční obor nerovnice D=(\frac{3}{5},+\infty).
  • Porovnáme argumenty logaritmů na obou stranách nerovnice. Protože je základ logaritmu menší než jedna, otáčíme znak nerovnosti.
  • Získáme nerovnici x+5\geq 5x-3, která je ekvivalentní s nerovnicí x\leq 2.
  • Na číselné ose určíme průnik definičního oboru a řešení předchozí nerovnice.
  • Množina všech kořenů původní nerovnice K=(\frac{3}{5},2>.

Zápis řešení:

Cvičení 7.1
Řešte nerovnice s neznámou x, y \in R:
\log_\frac{1}{2}(3x+4)\geq \log_\frac{1}{2}(x+8) \log_3(2y-2)\geq \log_3 (4y+2)
D=(-\frac{4}{3},+\infty)
D=(1,+\infty)
3x+4\leq x+8
2y-2\geq 4y+2
2x\leq 4
-2y \geq 4
x\leq 2
y \leq -2
K=(-\frac{4}{3},2)
K=\emptyset
NAHORU
Převod čísla na logaritmus

Opět se může stát, že na jedné straně nerovnice se místo logaritmu nachází číslo. Potom musíme toto číslo nejprve převést na logaritmus o základu, který se vyskytuje v nerovnici. Řešení takové nerovnice ukážeme v následujícím příkladu.

Příklad 7.2
Řešte nerovnici s neznámou x \in R:

\log_\frac{1}{10}(x+3)>-1

Řešení
  • Výrazy v nerovnici jsou definovány, pokud je splněna podmínka x+3>0.
  • Definiční obor nerovnice D=(-3,+\infty).
  • Nejprve převedeme výraz na pravé straně nerovnice na logaritmus o základu \frac{1}{10}, abychom mohli porovnat argumenty:
    -1=\log_\frac{1}{10} 10 .
  • Porovnáme argumenty logaritmů na obou stranách nerovnice. Protože je základ logaritmu menší než jedna, otáčíme znak nerovnosti.
  • Získáme nerovnici x+3<10, která je ekvivalentní s nerovnicí x < 7.
  • Na číselné ose určíme průnik definičního oboru a řešení předchozí nerovnice.
  • Množina všech kořenů původní nerovnice K=(-3,7).

Zápis řešení:

Cvičení 7.2
Řešte nerovnice s neznámou x, y \in R:
\log_3(x+2) \leq 3 \log_\frac{4}{7}(5-y)>0
D=(-2,+\infty)
D=(-\infty,5)
\log_3(x+2) \leq \log_3 27
\log_\frac{4}{7}(5-y)>\log_\frac{4}{7} 1
x+2 \leq 27
5-y < 1
x \leq 25
-y < -4
K=(-2,25>
y > 4
K=(4,5)
NAHORU
Složitější argument

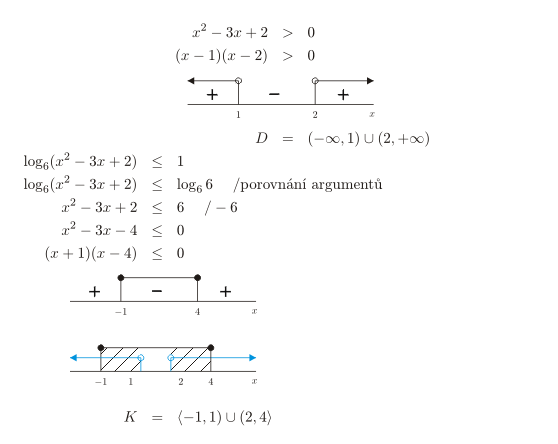
Zatím se v argumentech logaritmů vyskytovala neznámá pouze v první mocnině a po porovnání argumentů vznikla lineární nerovnice. V dalším příkladu ukážeme, že stejným způsobem se řeší i logaritmické nerovnice, kde je v argumentu logaritmu složitější výraz. Musíme si však dát pozor na určování definičního oboru a určování množiny všech kořenů.

Příklad 7.3
Řešte nerovnici s neznámou x \in R:

\log_6(x^2-3x+2)\leq 1

Řešení
  • Výrazy v nerovnici jsou definovány, pokud je splněna podmínka x^2-3x+2>0.
  • Podmínku převedeme na součinový tvar (x-1)(x-2)>0 a vyřešíme s pomocí číselné osy.
  • Definiční obor nerovnice D=(-\infty,1)\cup(2,+\infty).
  • Nejprve převedeme výraz na pravé straně nerovnice na logaritmus o základu 6, abychom mohli porovnat argumenty:
    1=\log_6 6 .
  • Porovnáme argumenty logaritmů na obou stranách nerovnice. Protože je základ logaritmu větší než jedna, neotáčíme znak nerovnosti.
  • Získáme nerovnici x^2-3x+2\leq 6, která je ekvivalentní s nerovnicí x^2-3x-4\leq 0.
  • Nerovnici převedeme na součinový tvar (x+1)(x-4)\leq 0 a vyřešíme na číselné ose. Řešením je interval (-1,4).
  • Na číselné ose určíme průnik definičního oboru a řešení předchozí nerovnice.
  • Množina všech kořenů původní nerovnice K=<-1,1)\cup(2,4>.

Zápis řešení:

NAHORU
Vícenásobné logaritmy

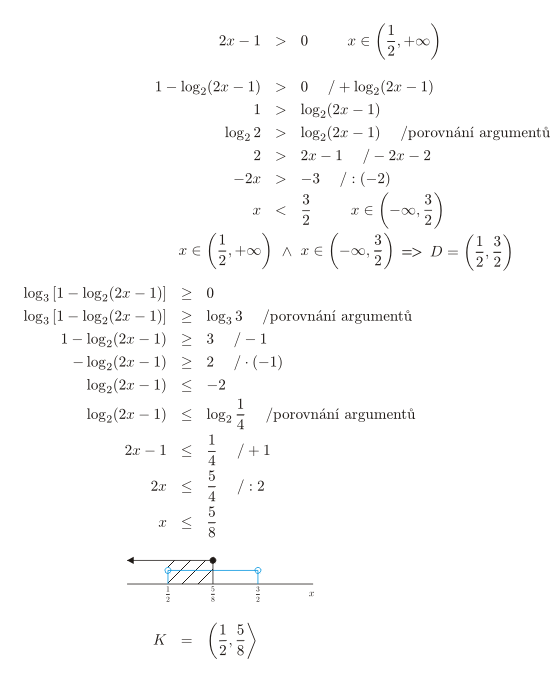
Stejně jako při řešení logaritmický rovnic můžeme řešit i logaritmické nerovnice, kde se v argumentech logaritmu nachází další logaritmus. U takové rovnice jsme neurčovali její definiční obor a na závěr příkladu jsme udělali zkoušku. U nerovnic takovou možnost nemáme a definiční obor určit musíme. Určit definiční obor ovšem znamená řešit další logaritmickou nerovnici, jak je vidět v následujícím příkladu.

Příklad 7.4
Řešte nerovnici s neznámou x \in R:

\log_3[1-\log_2(2x-1)]\geq 0

Řešení
  • Výrazy v nerovnici jsou definovány, pokud jsou splněny podmínky
    2x-1>0 a 1-\log_2(2x-1)> 0.
  • První podmínka je splněna pro x\in(\frac{1}{2},+\infty).
  • Nerovnici 1-\log_2(2x-1)> 0 řešíme porovnáním argumentů.
  • Logaritmus převedeme na pravou stranu rovnice a číslo 1 převedeme na logaritmus o základu 2, abychom mohli porovnat argumenty:
    1=\log_2 2 .
  • V nerovnici \log_2 2> \log_2(2x-1) porovnáme argumenty logaritmů na obou stranách nerovnice. Protože je základ logaritmu větší než jedna, neotáčíme znak nerovnosti.
  • Získáme nerovnici 2>2x-1, která je ekvivalentní s nerovnicí x < \frac{3}{2}.
  • Druhá podmínka je splněna pro x\in(-\infty,\frac{3}{2}).
  • Obě podmínky jsou splněny pro x\in(\frac{1}{2},\frac{3}{2}) (průnik intervalů). Definiční obor
    nerovnice D=(\frac{1}{2},\frac{3}{2}).
  • Nyní přístoupíme k řešení samotné nerovnice. Nejprve převedeme číslo 0 na logaritmus o základu 3, abychom mohli porovnat argumenty:
    0=\log_3 1 .
  • Porovnáme argumenty logaritmů na obou stranách nerovnice. Protože je základ logaritmu větší než jedna, neotáčíme znak nerovnosti.
  • Získáme nerovnici 1-\log_2 (2x-1)\geq 3, která je ekvivalentní s nerovnicí
    \log_2 (2x-1) \leq -2.
  • Převedeme číslo -2 na logaritmus o základu 2, abychom mohli znovu porovnat argumenty:
    -2=\log_2 \frac{1}{4} .
  • Porovnáme argumenty logaritmů na obou stranách nerovnice. Protože je základ logaritmu větší než jedna, neotáčíme znak nerovnosti.
  • Získáme nerovnici 2x-1\leq \frac{1}{4}, která je ekvivalentní s nerovnicí x\leq \frac{5}{8}.
  • Na číselné ose určíme průnik definičního oboru a řešení předchozí nerovnice.
  • Množina všech kořenů původní nerovnice K=(\frac{1}{2},\frac{5}{8}>.

Zápis řešení:

NAHORU