Logaritmická funkce

Zavedení logaritmické funkce

V předchozí kapitole jsme si představili exponenciální funkci. Nyní se pokusíme najít funkci, která je inverzní k exponenciální funkci.

Budeme vycházet z předpisu pro exponenciální funkci a vyjádříme nezávislou proměnou x pomocí y, tím získáme předpis pro inverzní funkci. Stejný postup byl ukázán v příkladu 3.2.

Pomocí základních matematických operací, umocňování a odmocňování se nám nepovede z předpisu y=a^x proměnnou x vyjádřit. Proto využijeme definici logaritmu pro přípustné hodnoty:

\log_a{r}=v~~\Leftrightarrow~~a^v=r,

pomocí které získáme předpis inverzní funkce k exponenciální funkci:

Tím jsme získali funkci y=\log_a{x}, která je inverzní k exponenciální funkci y=a^x. Tuto funkci budeme nazývat logaritmickou funkcí o základu a.

Logaritmická funkce o základu a \in R^+ - \{1\} je každá funkce na množině
R^+ zapsaná ve tvaru
y=\log_a{x}.

NAHORU
Graf logaritmické funkce

Z předpisu funkce y=\log_2{x} odvodíme, jak vypadá její graf. Samostatně dopočítejte funkční hodnoty v následující tabulce:

x -1 0 0,25 0,5 1 2 4 8
y=\log_2{x}
nelze
nelze
-2
-1
0
1
2
3

V kapitole o logaritmech jsme zjistili, že argument logaritmu musí být číslo větší než nula. Proto jsme nemohli určit první dvě funkční hodnoty v tabulce.

Nakreslíme graf funkce y=\log_2{x}.

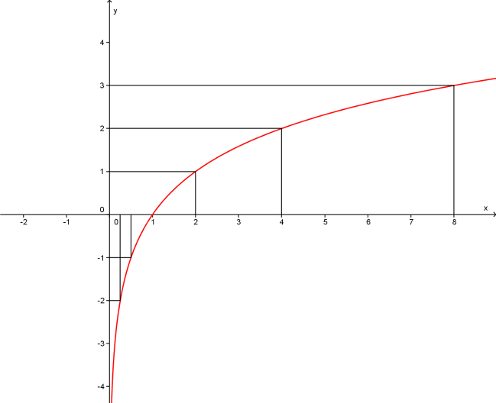
Logaritmická funkce je inverzní k funkci exponenciální, proto grafy funkcí y=\log_2{x} a y=2^x jsou osově souměrné podle osy y=x.

NAHORU
Vliv základu na graf logaritmické funkce

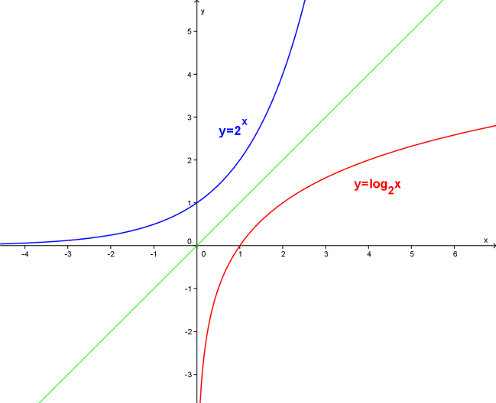
Nejprve v appletu opět zkuste měnit velikost základu a pozorujte, jak se mění graf logaritmické funkce:

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Na základě pozorování appletu doplňte:

NAHORU
Vlastnosti logaritmické funkce
Logaritmická funkce f: y=\log_{a}{x}, a>0, a\neq 1
Definiční obor D(f)=(0,+\infty)
Obor hodnot H(f)=R
Rostoucí pro a>1
Klesající pro a \in (0,1)
Prostá pro všechny přípustné základy
NAHORU
Porovnání logaritmů

Následující applet nám bude sloužit k porovnávání dvou logaritmů o stejném základu.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com
Poznámka

Užití appletu si ukážeme na jednoduchém příkladu.

Příklad 3.6
Rozhodněte, který z následujících logaritmů je větší:

\log_2 2~?~\log_2 4

Řešení
    Využijeme applet:
  • Na modrém posuvníku nastavíme hodnotu základu a=2.
  • Na červeném posuvníku nastavíme velikost prvního argumentu x_1=2.
    První logaritmus y_1=\log_2 2=1.
  • Na zeleném posuvníku nastavíme velikost druhého argumentu x_2=4.
    Druhý logaritmus y_2=\log_2 4=2.
  • Z grafu je vidět, že y_1 < y_2 , proto \log_2 2<\log_2 4.
Zápis řešení:

\log_2 2~?~\log_2 4 \rightarrow \log_2 2=1, \log_2 4=2, proto \log_2 2<\log_2 4

Cvičení 3.6
Rozhodněte, který z následujících logaritmů je větší:
\log_{0,5} 0,8~?~\log_{0,5} 3
\log_{0,5} 0,8=0,32
\log_{0,5} 3=-1,58
\log_{0,5} 0,8>\log_{0,5} 3
\log_{1,7} 0,5~?~\log_{1,7} 6
\log_{1,7} 0,5=-1,31
\log_{1,7} 6=3,38
\log_{1,7} 0,5<\log_{1,7} 6
\log_{4} 0,7~?~\log_{4} 0,3
\log_{4} 0,7=-0,26
\log_{4} 0,3=0,81
\log_{4} 0,7>\log_{4} 0,3
\log_{0,3} 1,5~?~\log_{0,3} 4
\log_{0,3} 1,5=-0,34
\log_{0,3} 4=-1,15
\log_{0,3} 1,5>\log_{0,3} 4

Při řešení předchozího cvičení jsme si mohli všimnout následujících zákonitostí při porovnání dvou logaritmů se stejným základem (opět jde o porovnání argumentů rostoucí a klesající funkce ).

    Je-li základ logaritmu
  • a \in (0,1), potom když je
    • první argument menší než druhý, je první logaritmus větší než druhý.
    • první argument větší než druhý, je první logaritmus menší než druhý.
  • a >1, potom když je
    • první argument menší než druhý, je první logaritmus menší než druhý.
    • první argument větší než druhý, je první logaritmus větší než druhý.
NAHORU