Substituce
Některé logaritmické nerovnice se nám nepovede upravit na tvar, ve kterém lze porovnat argumenty. Takové příklady můžeme řešit pomocí substituce, kterou jsme zavedli v kapitole o exponenciálních rovnicích. Postup řešení i použité značení jsme již tedy vysvětlili dříve.
Substituce za logaritmus
Příklady, které jsou uvedeny v této kapitole, se dají vždy řešit vhodnou stubstitucí nové neznámé za logaritmus. V jednotlivých příkladech ukážeme, jak z řešení nerovnice s novou neznámou získáme původní řešení nerovnice.
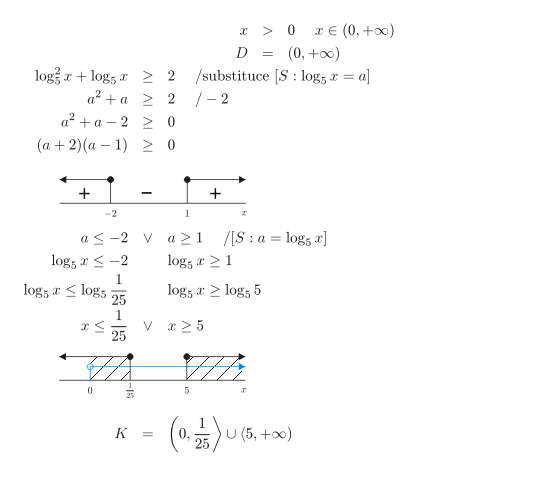
Řešte nerovnici s neznámou x \in R:
- Výrazy v nerovnici jsou definovány, pokud je splněna podmínka x>0.
- Definiční obor nerovnice D=(0,+\infty).
- V nerovnici \log^2_5 x + \log_5 x \geq 2 nahradíme všechny výrazy \log_5 x novou neznámou a.
- Nerovnici a^2 + a \geq 2 s neznámou a \in R vyřešíme.
- Nerovnici převedeme na součinový tvar (a+2)(a-1)\geq 0 a vyřešíme s pomocí číselné osy. Řešením je sjednocení intervalů (-\infty,-2>\cup<1,+\infty).
- Pro neznámou a tak dostáváme podmínky:
a\leq-2 nebo a\geq1. - Zpětně nahradíme neznámou a výrazem \log_5 x.
- Pro neznámou x dostáváme podmínky:
\log_5 x \leq-2 nebo \log_5 x \geq 1. - Nerovnice vyřešíme porovnáním argumentů:
x\leq \frac{1}{25} nebo x \geq 5. - Na číselné ose určíme průnik definičního oboru a řešení předchozích nerovnic.
- Množina všech kořenů původní nerovnice K=(0,\frac{1}{25}>\cup<5,+\infty).
Zápis řešení:
Řešte nerovnici s neznámou x \in R:
- Výrazy v nerovnici jsou definovány, pokud jsou splněny podmínky x>0 a \log_\frac{1}{2} x\neq 0.
- Definiční obor nerovnice D=(0,1)\cup(1,+\infty).
- V nerovnici \frac{2+\log_\frac{1}{2} x}{\log_\frac{1}{2} x}< 3 nahradíme všechny výrazy \log_\frac{1}{2} x novou neznámou a.
- Nerovnici \frac{2+a}{a}<3 s neznámou a \in R vyřešíme.
- Od obou stran nerovnice odečteme číslo 3, abychom porovnávali výraz na levé straně rovnice s nulou. Následně převedeme výraz na levé straně nerovnice na společného jmenovatele a získáme podílový tvar nerovnice:
\frac{2-2a}{a}<0, který vyřešíme s pomocí číselné osy. - Řešením je sjednocení intervalů (-\infty,0>\cup<1,+\infty).
- Pro neznámou a tak dostáváme podmínky:
a<0 nebo a>1. - Zpětně nahradíme neznámou a výrazem \log_\frac{1}{2} x.
- Pro neznámou x dostáváme podmínky:
\log_\frac{1}{2} x<0 nebo \log_\frac{1}{2} x >1. - Nerovnice vyřešíme porovnáním argumentů:
x> 1 nebo x < \frac{1}{2}. - Na číselné ose určíme průnik definičního oboru a řešení předchozích nerovnic.
- Množina všech kořenů původní nerovnice K=(0,\frac{1}{2})\cup(1,+\infty).
Zápis řešení:

Řešte nerovnici s neznámou x \in R:
- Výrazy v nerovnici jsou definovány, pokud je splněna podmínka x+2>0.
- Definiční obor nerovnice D=(-2,+\infty).
- V nerovnici \log^2_\frac{1}{3}(x+2)-3\log_\frac{1}{3}(x+2)\leq 0 nahradíme všechny výrazy \log_\frac{1}{3}(x+2) novou neznámou a.
- Nerovnici a^2 - 3a \leq 0 s neznámou a \in R vyřešíme.
- Nerovnici převedeme na součinový tvar a(a-3)\leq 0 a vyřešíme s pomocí číselné osy. Řešením je interval <0,3>.
- Pro neznámou a tak dostáváme podmínky:
a\geq 0 a zároveň a\leq 3 . - Zpětně nahradíme neznámou a výrazem \log_\frac{1}{3}(x+2).
- Pro neznámou x dostáváme podmínky:
\log_\frac{1}{3}(x+2)\geq 0 a zároveň \log_\frac{1}{3}(x+2)\leq 3 . - Nerovnice vyřešíme porovnáním argumentů:
x\leq -1 a zároveň x \geq -\frac{53}{27}. - Na číselné ose určíme průnik definičního oboru a řešení předchozích nerovnic.
- Množina všech kořenů původní rovnice K=<-\frac{53}{27},-1>.
Zápis řešení:
