Logaritmus
V matematice se setkáváme se situací, kdy rovnost mezi čísly můžeme vyjádřit různými způsoby. Ukážeme si vztah mezi mocninou a odmocninou:
Z rovnosti 3^2=9 plyne rovnost \sqrt[2]{9}=3,
z rovnosti 5^3=125 plyne rovnost \sqrt[3]{125}=5.
Nyní zavedeme ještě další zápis pro mocninu
pro které platí: a^v=r.
Číslo a nazýváme základ logaritmu,
číslo r nazýváme argument logaritmu,
číslo v nazýváme logaritmus.
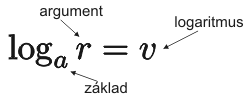
- a) 2^3=8
- b) 3^{(-2)}=\frac{1}{9}
- c) 25^{\frac{1}{2}}=5
Využijeme definici logaritmu \log_a{r}=v~~\Leftrightarrow~~a^v=r.
- a)
- Základ mocniny a=2 použijeme jako základ logaritmu,
- exponent v=3 jako logaritmus,
- mocninu r=8 jako argument logaritmu.
- Zapíšeme výsledek: \log_2{8}=3.
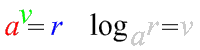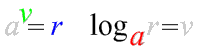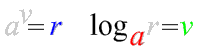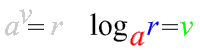
Zápis řešení:
- a) \log_2{8}=3
- b) \log_3{\frac{1}{9}}=-2
- c) \log_{25}{5}=\frac{1}{2}
| 2^5=32 | \log_2{32}=5
|
10^3=1~000 | \log_{10}{1~000}=3 |
| 7^0=1 | \log_7{1}=0 |
3^{-3}=\frac{1}{27} | \log_3{\frac{1}{27}}=-3 |
| 16^{\frac{1}{4}}=2 | \log_{16}{2}=\frac{1}{4} |
(\frac{1}{3})^{-2}=9 | \log_{\frac{1}{3}}{9}=-2 |
Nejprve se naučíme určovat logaritmy daných základů a argumentů.
|
|
- a)
- Hledané číslo si označíme symbolem ?: \log_3{9}=?.
- Přepíšeme rovnost pomocí definice logaritmu \log_a{r}=v~~\Leftrightarrow~~a^v=r tj. 3^?=9.
- Určíme hledané číslo. Ptáme se, na kolikátou musíme umocnit číslo 3, abychom získali číslo 9.
- Snadno uhodneme, že hledané číslo je 2, protože 3^2=9.
- Zapíšeme výsledek: \log_3{9}=2.

Zápis řešení:
- a) \log_3{9}=? \rightarrow 3^?=9 \rightarrow ?=2, proto \log_3{9}=2
- b) \log_2{16}=? \rightarrow 2^?=16 \rightarrow ?=4, proto \log_2{16}=4
- c) \log_6{\frac{1}{36}}=? \rightarrow 6^?=\frac{1}{36} \rightarrow ?=-2, proto \log_6{\frac{1}{36}}=-2
- d) \log_8{2}=? \rightarrow 8^?=2 \rightarrow ?=\frac{1}{3}, proto \log_8{2}=\frac{1}{3}
| \log_7{7}=? | 7^?=7 |
?=1 |
\log_7{7}=1 |
| \log_4{16}=? | 4^?=16 |
?=2 |
\log_4{16}=2 |
| \log_{11}{1}=? | 11^?=1 |
?=0 |
\log_{11}{1}=0 |
| \log_2{\frac{1}{8}}=? | 2^?=\frac{1}{8} |
?=-3 |
\log_2{\frac{1}{8}}=-3 |
| \log_{\frac{1}{3}}{9}=? | (\frac{1}{3})^?=9 |
?=-2 |
\log_{\frac{1}{3}}{9}=-2 |
| \log_9{3}=? | 9^?=3 |
?=\frac{1}{2} |
\log_9{3}=\frac{1}{2} |
| \log_{\frac{2}{7}}{\frac{7}{2}}=? | (\frac{2}{7})^?=\frac{7}{2} |
?=-1 |
\log_{\frac{2}{7}}{\frac{7}{2}}=-1 |
| \log_{\frac{1}{4}}{0,5}=? | (\frac{1}{4})^?=0,5 |
?=\frac{1}{2} |
\log_{\frac{1}{4}}{0,5}=\frac{1}{2} |
Při řešení logaritmických a exponenciálních rovnic bude třeba určit neznámý základ či argument logaritmu. V následujícím příkladu se naučíme základy a argumenty logaritmů počítat.
- a) \log_x{16}=4
- b) \log_8{x}=\frac{1}{3}
- a) Nejprve ukážeme, jak vypočítat základ logaritmu v rovnosti \log_x{16}=4.
- Přepíšeme rovnost podle definice logaritmu \log_a{r}=v~~\Leftrightarrow~~a^v=r.
\log_x{16}=4~~\Leftrightarrow~~x^4=16 - Řešení této rovnice můžeme uhodnout nebo ji vyřešit odmocněním: x=\sqrt[4]{16}=2.
- Zapíšeme výsledek: x=2.
- b) V rovnosti \log_8{x}=\frac{1}{3} vypočítáme argument logaritmu.
- Opět přepíšeme rovnost podle definice logaritmu \log_a{r}=v~~\Leftrightarrow~~a^v=r.
\log_8{x}=\frac{1}{3}~~\Leftrightarrow~~8^{\frac{1}{3}}=x - Z této rovnice přímo vidíme, jak vypočítat neznámou x=8^{\frac{1}{3}}=2.
- Zapíšeme výsledek x=2.
- a) \log_x{16}=4 \rightarrow x^4=16 \rightarrow x=2
- b) \log_8{x}=\frac{1}{3} \rightarrow 8^{\frac{1}{3}}=x \rightarrow x=2
| \log_x{8}=1 | x^1=8 |
x=8 |
| \log_3{x}=4 | 3^4=x |
x=81 |
| \log_5{x}=0 | 5^0=x |
x=1 |
| \log_x{\frac{1}{4}}=2 | x^2=\frac{1}{4} |
x=\frac{1}{2} |
| \log_x{125}=-3? | x^{-3}=125 |
x=\frac{1}{5} |
| \log_{\frac{1}{4}}{x}=-3? | (\frac{1}{4})^{-3}=x |
x=64 |
Ve cvičeních 2.2 a 2.3 jsme se setkali s několika příklady, kdy byl logaritmus roven nule nebo jedné. Než začnete číst další odstavec, zkuste se podívat, co měly tyto příklady společného.
- Logaritmus byl roven nule, pokud agrumnet logaritmu byl roven jedné.
- Logaritmus byl roven jedné, pokud základ i argument logaritmu byl stejný.
Již jsme zjistili, kdy je logaritmus roven nule nebo jedné. V následující tabulce přehledně uvedeme, jakých hodnot logaritmus nabývá v závislosti na základu a argumentu logaritmu.
| a \in (0,1) | a \in (1,+\infty) | ||
|---|---|---|---|
| r | \log_a{r} | r | \log_a{r} |
| (0,a) | (1,+\infty) | (0,1) | (-\infty,0) |
| \{a\} | \{1\} | \{1\} | \{0\} |
| (a,1) | (0,1) | (1,a) | (0,1) |
| \{1\} | \{0\} | \{a\} | \{1\} |
| (1,+\infty) | (-\infty,0) | (a,+\infty) | (1,+\infty) |
- a) \log_{12}{3}
- b) \log_{\frac{2}{3}}{\frac{3}{5}}
- Základ je z intervalu (0,1).
- Je-li argument menší než jedna, je logaritmus kladné číslo.
- Je-li argument větší než jedna, je logaritmus záporné číslo.
-
Základ je z intervalu (1,+\infty).
- Je-li argument menší než jedna, je logaritmus záporné číslo.
- Je-li argument větší než jedna, je logaritmus kladné číslo.
a) Pro \log_{12}{3} je základ větší než 1 a zároveň argument je větší než 1. Logaritmus proto nabývá kladné hodnoty.
b) Pro \log_{\frac{2}{3}}{\frac{3}{5}} je základ menší než 1 a zároveň argument je menší než 1. Logaritmus proto nabývá kladné hodnoty.
| \log_{7}{\frac{1}{4}} | záporné |
\log_{\frac{1}{4}}{\frac{1}{6}} | kladné |
| \log_{2}{0,2} | záporné |
\log_{0,4}{1,3} | záporné |
Na závěr této kapitoly se budeme věnovat dvěma nejčastěji používaným logaritmům - dekadickému a přirozenému.
Dekadický logaritmus je logaritmus o základu 10. Byl využíván zejména v době, kdy se používala logaritmická pravítka a tabulky logaritmů k výpočtům složitějších matematický operací (více se o tom zmíníme v kapitole o využití logaritmů v praxi). Základ 10 nebyl zvolen náhodou, ale vycházel ze skutečnosti, že lidé počítají v desítkové soustavě. Dekadický logaritmus je hojně využíván, a proto se zkrátil jeho zápis. Místo
Přirozený logaritmus je logaritmus se základem e. Číslo e je iracionální (podobně jako číslo \pi) a nazývá se Eulerovo číslo. Jeho přibližná hodnota je 2,71. Tento logaritmus je také hojně využíván, a proto byla pro jeho zápis opět vytvořena zkratka. Místo
Dekadické a přirozené logaritmy jsou často používány, a proto obsahují kalkulačky funkci na počítání těchto logaritmů (ostatní logaritmy můžeme pomocí těchto logaritmů vypočítat, jak bude ukázáno v následující kapitole).

- a) \log{25}
- b) \ln{7}
Na kalkulačce zvolíme funkci log nebo ln. Jako argument logaritmu zadáme příslušné číslo.
 Zápis řešení:
Zápis řešení:
- a) \log{25}=1,397~9
- b) \ln{7}=1,945~9
| \log{156}= | 2,193~1 |
\log{3,1}= | 0,491~4 |
| \ln{24}= | 3,178~1 |
\ln{0,5}= | -0,693~1 |