Osová afinita v rovině
Osovou afinitu v rovině si zavedeme pomocí rovnoběžného promítání a osové afinity mezi rovinami.
Definice
Mějme dánu osovou afinitu mezi různoběžnými rovinami α, β, která je určena osou p a uspořádanou dvojicí bodů MM', kde M je libovolný bod ležící v rovině α a M' je jeho obraz ležící v rovině β. Dále je dáno rovnoběžné promítání do průmětny π směrem m, m π, přičemž π
π, přičemž π MM'. Průměty bodů M, M' do roviny π jsou po řadě body L, L'; průmět osy p je přímka o.
MM'. Průměty bodů M, M' do roviny π jsou po řadě body L, L'; průmět osy p je přímka o.
Osová afinita v rovině π s osou o je zobrazení, ve kterém se bod L zobrazí do bodu L'.
Osovou afinitu v rovině také získáme jako rovnoběžný průmět osové afinity mezi rovinami α, β do roviny π.
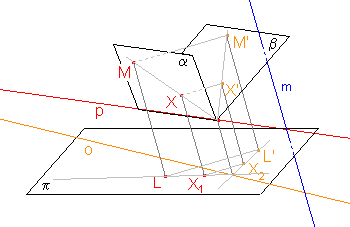
Rovnoběžný průmět osové afinity
Osová afinita v rovině π je určena osou o a uspořádanou dvojicí bodů LL'.
Body LL' určují směr osové afinity.
Ze zavedení osové afinity v rovině vyplývá, že vlastnosti osové afinity v rovině jsou stejné jako u rovnoběžného promítání.
Poznámky
- Body L, L', pomocí kterých je zadána osová afinita, neleží na ose afinity.
- Vzor a obraz přímky, která je různoběžná s osou, se protínají na ose afinity.
Další vlastnosti
- V osové afinitě v rovině je:
- a) obrazem přímky opět přímka;
- b) obrazem roviny opět rovina;
- c) obrazem úsečky AB úsečka A'B';
- d) obrazem polopřímky AB polopřímka A'B';
- e) obrazem trojúhelníku ABC trojúhelník A'B'C';
- f) obrazem středu úsečky AB střed úsečky A'B'.
- V osové afinitě v rovině se zachovává rovnoběžnost přímek, tj. dvě navzájem rovnoběžné přímky p, q se zobrazí na dvě navzájem rovnoběžné přímky p', q'.
- Osa afinity je množina všech samodružných bodů.
- Jsou-li body P, Q v osové afinitě v rovině π dva různé samodružné body, potom každý bod přímky PQ je samodružný a jedná se o osu afinity.
- V osové afinitě v rovině π se přímky, které jsou rovnoběžné se směrem afinity, zobrazí samy na sebe. Říkáme jim samodružné přímky.
Samodružná přímka není totéž co přímka samodružných bodů. Přímka samodružných bodů zobrazuje každý bod sám na sebe, tj. každý bod této přímky je samodružný, ale samodružná přímka znamená, že její body se zobrazí na jiný její bod (jednotlivé body nejsou samodružné, ale přímka se zobrazí opět na tutéž přímku).
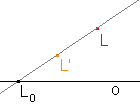
Podle směru s rozlišujeme následující případy osové afinity v rovině:
- kosoúhlá - s
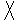 o
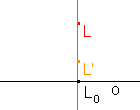
o - pravoúhlá - s
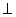 o
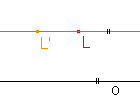
o - afinní elace - s
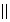 o
o
Pravoúhlou osovou afinitu s dělicím poměrem (LL'L0) = -1, kde bod L' je obraz bodu L a L0 je samodružný bod ležící na přímce LL', nazýváme osová souměrnost.
 |
 |
 |
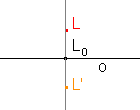 |
| kosoúhlá afinita | pravoúhlá afinita | afinní elace | osová souměrnost |
V případě, že vzor a obraz leží ve stejné polorovině vymezené osou o, jde o přímé zobrazení, jinak o nepřímé zobrazení. Osová souměrnost je příkladem nepřímého zobrazení, afinní elace přímého. Pro pochopení pojmu o přímých a nepřímých zobrazeních se můžete podívat na stránky Jiřího Doležala o Geometrických zobrazeních v rovině.
Příklad 1
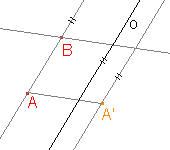
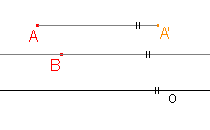
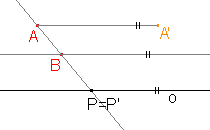
Je dána osová afinita v rovině osou o a uspořádanou dvojicí bodů AA'. Najděte obraz bodu B.
a) 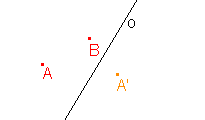 |
b) 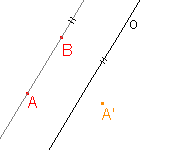 |
c) 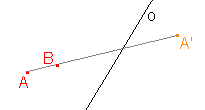 |
d) 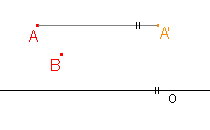 |
e) 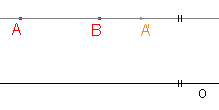 |
Řešení
a) 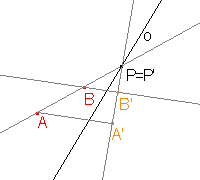 |
|
b) 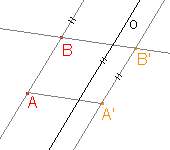 |
|
c) 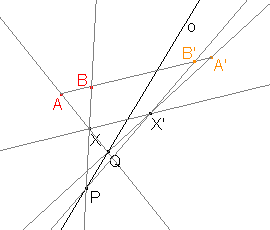 |
|
d) 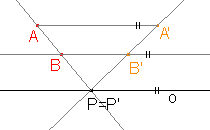 |
|
e)  |
|
Příklad 2
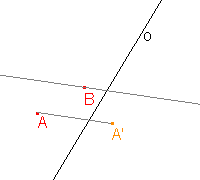
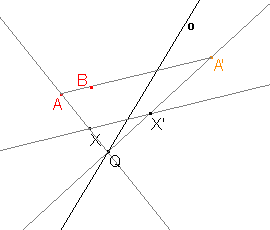
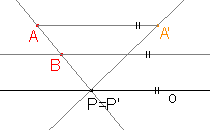
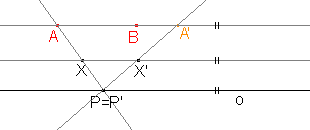
Určete osu a směr afinity, jestliže je osová afinita zadána třemi uspořádanými dvojicemi AA', BB', CC', jako je tomu na obrázku.
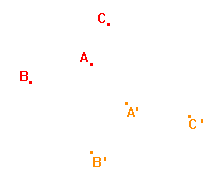
Řešení
Postup si ukážeme po krocích.
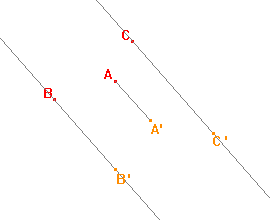 Přímky určené uspořádanými dvojicemi AA', BB', CC' jsou navzájem rovnoběžné, a tedy za směr afinity můžeme vzít některou z těchto tří přímek. |
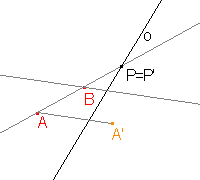
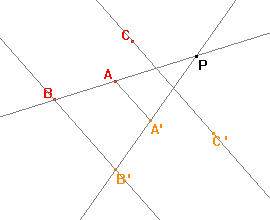 Přímka A'B' je obrazem přímky AB. Přímky jsou různoběžné, jejich průsečíkem je tedy bod P. Bod P je samodružný a bude ležet na hledané ose afinity. |
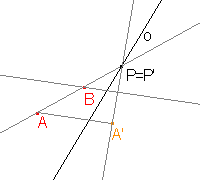
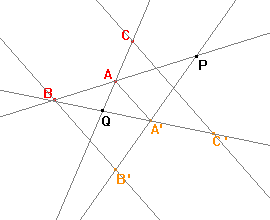 Stejně jako bod P můžeme sestrojit bod Q, který bude průsečíkem přímek AC a A'C' a který je také samodružný. |
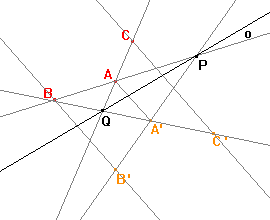 Osu afinity o sestrojíme pomocí bodů P a Q, protože jsou tyto body samodružné, a tudíž jistě leží na ose afinity. |
Úlohy
1. Osová afinita je zadána osou o a uspořádanou dvojicí bodů AA'. Určete obraz bodu B:
a) 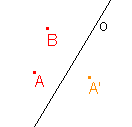 |
b) 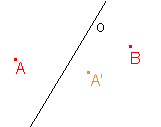 |
| Řešení | Řešení |
c) 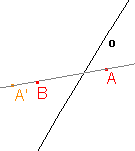 |
d) 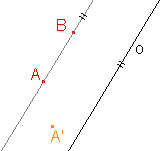 |
| Řešení | Řešení |
2. Osová afinita je zadána osou o a uspořádanou dvojicí bodů AA'. Určete obraz přímky p:
a) 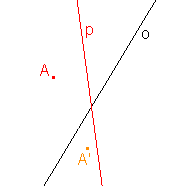 |
b) 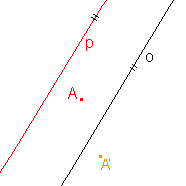 |
| Řešení | Řešení |
c) 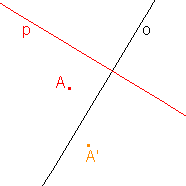 |
d) 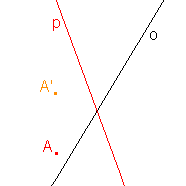 |
| Řešení | Řešení |
3. Osová afinita je zadána osou o a uspořádanou dvojicí bodů AA'. Určete obraz trojúhelníku ABC:
a) 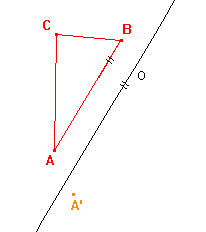 |
b) 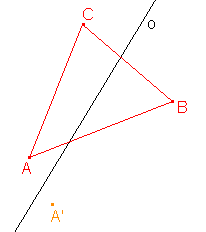 |
| Řešení | Řešení |
c) 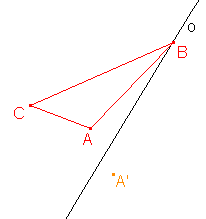 |
d) 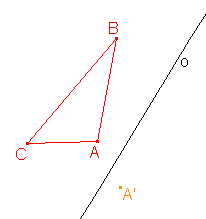 |
| Řešení | Řešení |
4. Určete osu a směr afinity, jestliže je osová afinita zadána třemi uspořádanými dvojicemi AA', BB', CC'.
a) 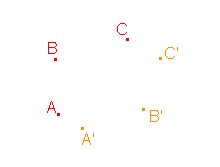 |
b) 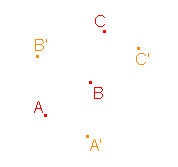 |
| Řešení | Řešení |
c) 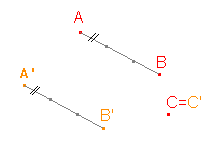 |
|
| Řešení |
5. Určete osu a směr afinity, jestliže je osová afinita zadána párem odpovídajících si přímek p, p' a uspořádanou dvojicí bodů AA'.
a) 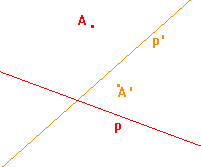 |
b) 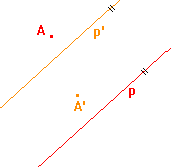 |
| Řešení | Řešení |
6. Určete osu a směr afinity, jestliže je osová afinita zadána dvěma páry odpovídajících si přímek p, p' a q, q'.
a) 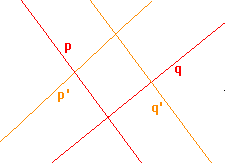 |
b) 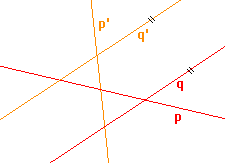 |
| Řešení | Řešení |