Stereometrie - afinita

Osová afinita mezi dvěma rovinami

Definice
Jsou dány roviny α a β a směr s, přičemž roviny α i β nejsou rovnoběžné se směrem s.
Osová afinita mezi různoběžnými rovinami α a β je rovnoběžné promítání bodů roviny α do roviny β směrem s.
Průsečnice rovin α a β se nazývá osa afinity.
Osová afinita mezi rovinami α a β je určena osou afinity o a uspořádanou dvojicí různých bodů LL', kde L je libovolný bod roviny α neležící na ose afinity a L' je jeho obraz v rovině β.

Poznámky

• Uspořádaná dvojice bodů LL' se nazývá směr osové afinity.
• Body L, L' neleží na ose afinity.
• Vzor a obraz přímky, která je různoběžná s osou, se protínají na ose afinity.

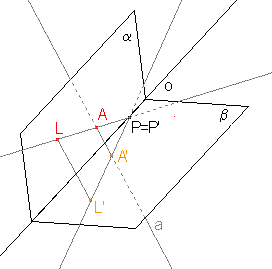
Z definice vyplývá, že vlastnosti osové afinity mezi dvěma rovinami jsou stejné jako u rovnoběžného promítání.

Další vlastnosti

1. V osové afinitě mezi rovinami α a β je:
   a) obrazem přímky opět přímka;
   b) obrazem roviny opět rovina;
   c) obrazem úsečky AB úsečka A'B';
   d) obrazem polopřímky AB polopřímka A'B';
   e) obrazem trojúhelníku ABC trojúhelník A'B'C';
   f) obrazem středu úsečky AB je střed úsečky A'B'.
2. Osa afinity je množina všech samodružných bodů.
3. V osové afinitě mezi různoběžnými rovinami se zachovává rovnoběžnost přímek, tj. dvě rovnoběžné přímky p, q se zobrazí na dvě rovnoběžné přímky p', q'.
4. Jsou-li body P, Q v osové afinitě mezi dvěma rovinami dva různé samodružné body, potom každý bod přímky PQ je samodružný a jedná se o osu afinity.

Využití
Osová afinita má široké využití, například v písmomalířství, deskriptivní geometrii a stavebnictví. My ji zde budeme využívat ke konstrukci řezů hranolů, kde rovina β je rovina řezu, rovina α je rovina stěny (nejčastěji podstavy) a s je směr bočních stěn, také ke konstrukci válců, kde rovina β je rovina řezu, rovina α je rovina podstavy a s je směr osy daného válce.

V následujících příkladech na osovou afinitu mezi rovinami α, β je vždy barevně vyznačena stěna ležící zadané rovině. Pokud jsou roviny zadány body neležících v jedné stěně tělesa, jsou barevně vyznačeny podstatné části rovin. Rovina α je vyznačena červenou barvou a rovina β oranžovou barvou.

Příklad 1
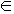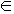Je dána krychle ABCDEFGH a osová afinita mezi rovinami α a β určená osou o a uspořádanou dvojicí bodů LL', kde L α, L' β.
Najděte obraz bodu X roviny α v rovině β, jestliže α= CDG a β= ADE

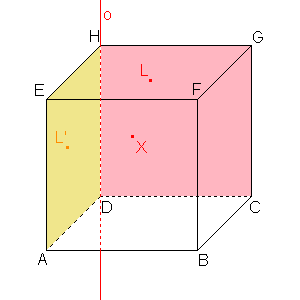
Řešení
Postup si ukážeme po krocích.

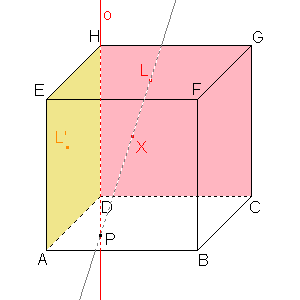Body L, X mohu vést přímku, která protne osu afinity v bodě P, který je samodružný.	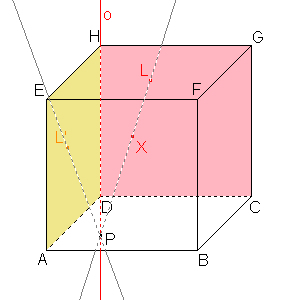Sestrojíme přímku, která prochází body L' a P a je obrazem přímky LX. Hledaný bod bude ležet na této přímce, a to díky zachování incidence.
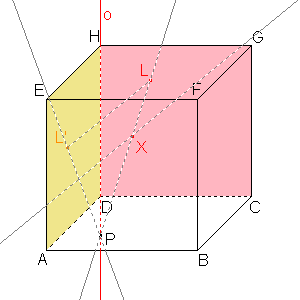Sestrojíme promítací přímku bodu X se směrem LL'.	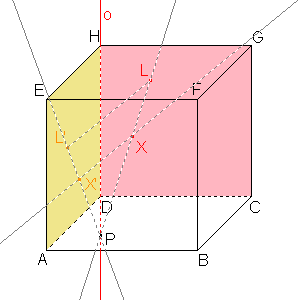Obrazem X' bodu X je průsečík rovnoběžky a přímky L'P.

Příklad 2
Mějme dánu krychli ABCDEFGH a roviny α= ABC a β= KLM, kde K, L, M jsou po řadě středy hran AE, BF, FG.
Najděte osu afinity mezi rovinami α a β.

Řešení
Průnik rovin α a β je osa afinity - přímka, která je množinou samodružných bodů. Při hledání osy afinity je tedy potřeba mít zadány dvě roviny, mezi kterými se zobrazuje, a směr afinity. Můžeme jej zvolit libovolně, ale různoběžně s rovinami afinity. Pro tuto úlohu vezměme směr kolmý na rovinu α, bod B je obrazem bodu L.
Řešení si ukážeme po krocích.

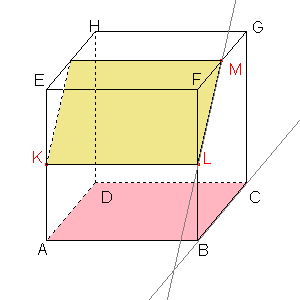Obrazem přímky dané body LM je přímka BC, protože obraz bodu L je bod B a obraz bodu M je střed úsečky BC.	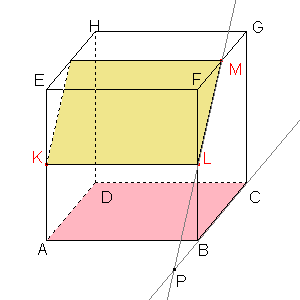Průsečíkem přímky LM a přímky BC je samodružný bod P, který leží na ose afinity.
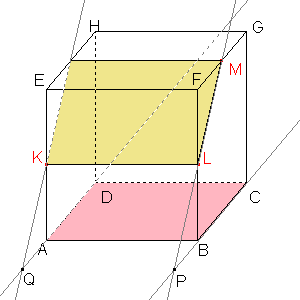Sestrojíme průsečík Q přímky AD a jejího vzoru.	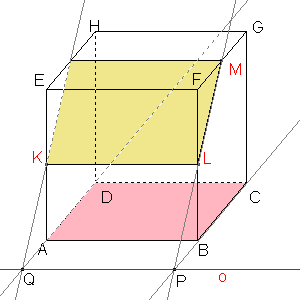Osa afinity prochází samodružnými body P, Q.

---

Úlohy

1. Je dána krychle ABCDEFGH a osová afinita mezi rovinami α a β určená osou o a uspořádanou dvojicí bodů LL', kde bod L 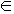α a bod L' 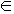β. Najděte obraz bodu X, X 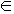α, jestliže:

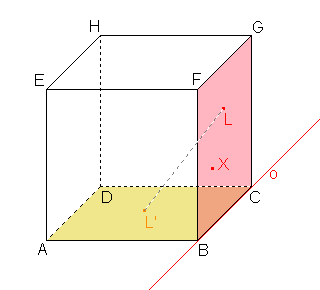a) α= BCG, β= ABC Řešení

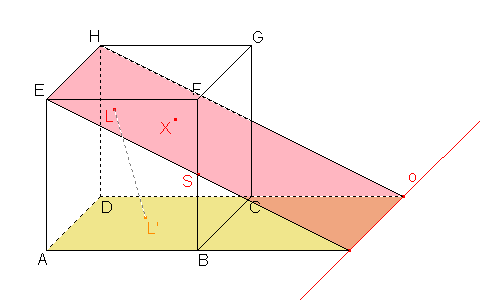b) α= EHS, S je střed hrany BF, β= ABC Řešení

2. Je dán šestiboký hranol ABCDEFGHIJKM a osová afinita mezi rovinami α a β určená osou o a uspořádanou dvojicí bodů LL', kde bod L 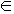α a bod L' 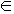β. Najděte obraz bodu X, X 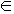α, jestliže:

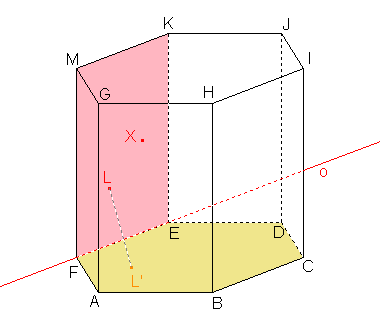a) α= EFK, β= ABC Řešení

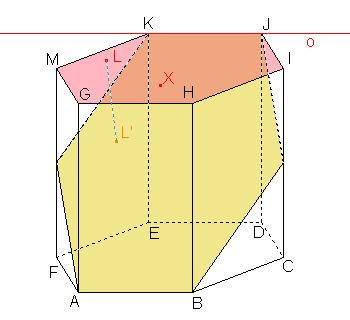b) α= GHI, β= ABJ Řešení

3. Je dána krychle ABCDEFGH. Najděte osu afinity mezi rovinami:

a) GCD, ABC

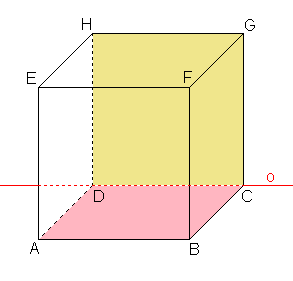
Skryj výsledek

Zobraz výsledek

b) ABC, KLH, kde K je střed hrany BF, L je střed hrany CG

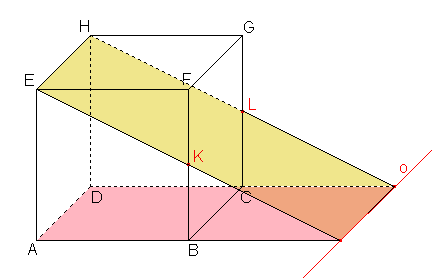
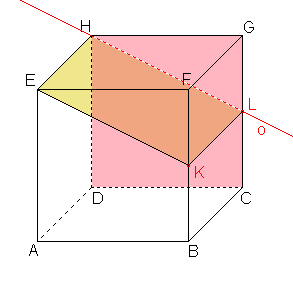
Skryj výsledek

Zobraz výsledek

c) CDG, KLH, kde K 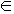BF, (BFK) = -1, L 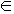CG, (CGL) = -1

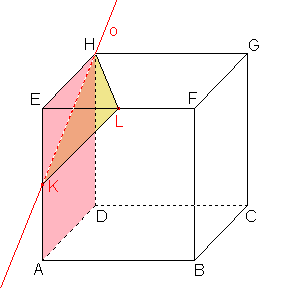
Skryj výsledek

Zobraz výsledek

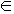d) ADH, KLH, kde K AE, (AEK) = -1, L 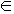EF, (EFL) = -1

Skryj výsledek

Zobraz výsledek

4. Je dána krychle ABCDEFGH. Najděte osu afinity mezi rovinami:

a) ABC, KLH, kde K AE, (AEK) = -1, L EF, (EFL) = -1
Řešení

b) BCG, KLH, kde K AE, (AEK) = -1, L EF, (EFL) = -1
Řešení

5. Je dán šestiboký hranol ABCDEFGHIJKM. Najděte osu afinity mezi rovinami:

a) GHI, AUV, kde U je střed hrany IC a V je střed hrany DJ
Řešení

b) HJU, kde U je střed úsečky CI; ABC
Řešení

↑