Tělesa
Nyní si tedy připomeneme některá tělesa, která budeme dále používat. Další tělesa naleznete v práci Lídy Kadlecové Stereometrie.
Hranoly
Vznik hranolu
Zvolme rovinu α a v ní libovolný n-úhelník. Dále zvolme přímku s různoběžnou s rovinou α. Sjednocení všech přímek rovnoběžných s přímkou s a protínajících n-úhelník se nazývá n-boký hranolový prostor. Tento hranolový prostor řízneme dvěma navzájem rovnoběžnými rovinami, které nejsou rovnoběžné s přímkou s. Průnikem těchto rovin s hranolovým prostorem jsou dva shodné n-úhelníky, tzv. podstavy hranolu, a část hranolového prostoru vymezená těmito rovinami se nazývá n-boký hranol. Úsečky spojující vrcholy podstav hranolu, které jsou rovnoběžné se směrem s, se nazývají boční hrany. Přímky hranolového prostoru, které protínají strany n-úhelníku podstavy tělesa, tvoří hranolovou plochu.
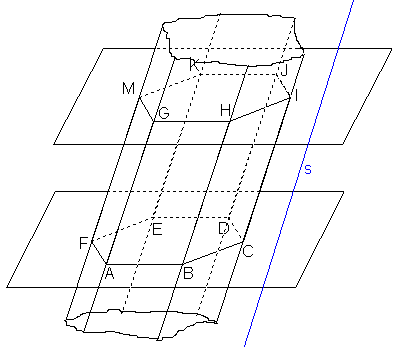
Hranoly dělíme na nekonvexní a konvexní:
- nekonvexní hranol - jeho podstavy jsou shodné nekonvexní mnohoúhelníky
- konvexní hranol - jeho podstavy jsou shodné konvexní mnohoúhelníky
- kosý hranol - boční hrany nejsou kolmé k podstavě
- kolmý hranol - boční hrany jsou kolmé k podstavě
| Název tělesa | Popis | Obrázek |
| Nekonvexní kosý hranol | podstavou je nekonvexní mnohoúhelník | 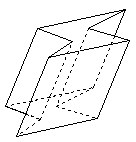 |
| Nekonvexní kolmý hranol | podstavou je nekonvexní mnohoúhelník a boční hrany jsou kolmé k podstavě | 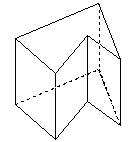 |
| Konvexní kosý hranol | podstavou je konvexní mnohoúhelník | 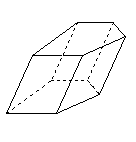 |
| Konvexní kolmý hranol | podstavou je konvexní mnohoúhelník a boční hrany jsou kolmé k podstavě | 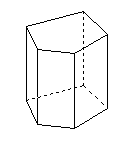 |
| Pravidelný šestiboký hranol | podstavy jsou pravidelné šestiúhelníky, boční stěny jsou obdélníky (případně čtverce) a boční hrany jsou kolmé k podstavě (jedná se tedy o kolmý hranol) | 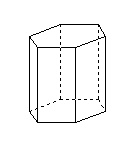 |
| Kvádr | podstavou je obdélník nebo čtverec a každé dvě protilehlé stěny jsou rovnoběžné a shodné (jedná se o kolmý čtyřboký hranol) | 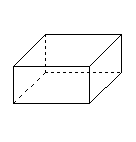 |
| Krychle | všechny stěny jsou shodné čtverce (jedná se o pravidelný kolmý čtyřboký hranol) | 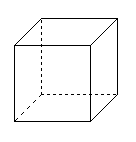 |
Válce
Vznik válce
Zvolme rovinu α a v ní libovolný kruh. Dále zvolme přímku s procházející středem kruhu a různoběžnou s rovinou α, tzv. osa válce. Sjednocení všech přímek rovnoběžných s přímkou s a protínajících kruh se nazývá válcový prostor. Válcový prostor řízneme dvěma navzájem rovnoběžnými rovinami, které nejsou rovnoběžné s přímkou s. Průnik těchto rovin s válcovým prostorem jsou kruhy, tzv. podstavy válce, a část válcového prostoru vymezená těmito rovinami se nazývá kruhový válec. Úsečky ležíci na plášti válce rovnoběžné s osou válce a mající koncové body na podstavách válce se nazývají strany válce. Přímky válcového prostoru, které protínají kružnici podstavy tělesa, tvoří válcovou plochu.
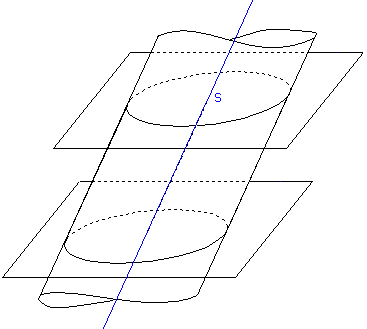
Válce dělíme na kolmé a kosé:
- kosý válec - osa válce není kolmá k podstavě
- kolmý válec - osa válce je kolmá k podstavě
| Název tělesa | Popis | Obrázek |
| Kosý kruhový válec | podstavy jsou shodné kruhy a osa válce není kolmá k podstavě | 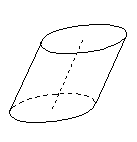 |
| Kolmý kruhový válec | podstavy jsou shodné kruhy a osa válce je kolmá na podstavu. | 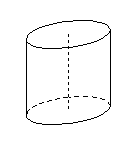 |
Poznámka
Kolmý kruhový válec nazýváme též rotační, neboť toto těleso také vzniká rotací obdélníku kolem jedné jeho strany.