Řezy hranolů
Řezem hranolu rovinou je mnohoúhelník, jehož vrcholy leží na hranách tělesa a jehož strany leží ve stěnách tělesa.
Řezy hranolů, resp. mnohostěnů, stejně jako základní objekty ze stereometrie, jsou již popsány v práci Stereometrie od Lídy Kadlecové. V její práci mimo jiné najdete výklad a několik příkladů ke konstrukci řezů mnohostěnů řešených pomocí tří základních stereometrických vět a jejich důsledků.
My si zde ukážeme, jak konstruovat řez hranolu rovinou pomocí osové afinity mezi rovinami, u některých příkladů si ukážeme i řešení pomocí tří základních vět a jejich důsledků.
Příklad 1
Sestrojte řez krychle ABCDEFGH rovinou BGX, kde bod X je střed hrany AE.
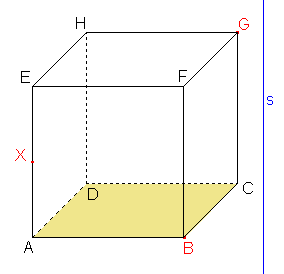
Řešení
Ukážeme si dva způsoby řešení - nejdříve pomocí osové afinity mezi rovinami a dále pomocí stereometrických vět a jejich důsledků.
a) Využijeme osové afinity mezi dvěma rovinami, a to rovinou řezu a rovinou dolní podstavy, za směr afinity s vezmeme směr bočních hran.
Postup si ukážeme po krocích.
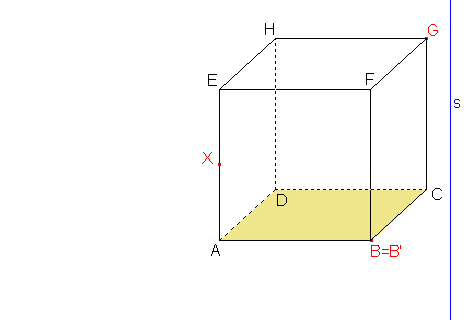 Nejprve musíme najít osu afinity, která je průsečnicí roviny dolní podstavy a roviny řezu dané body BGX. Bod B náleží oběma rovinám, je samodružný a leží tedy i na hledané ose afinity. |
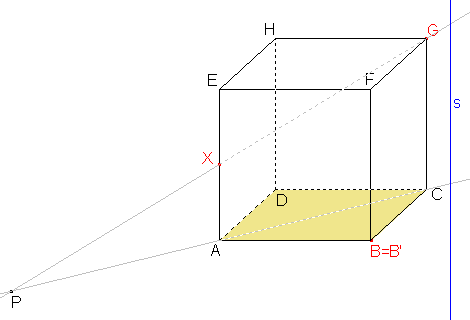 K sestrojení osy afinity budeme potřebovat dva body. Jeden bod již máme, bod B, a druhý získáme pomocí bodů X, G. Obrazem přímky XG v zadané osové afinitě je přímka AC, protože obrazem bodu X je bod A a bodu G je bod C. Průsečíkem přímky XG a přímky AC je samodružný bod P, který bude ležet na ose afinity. |
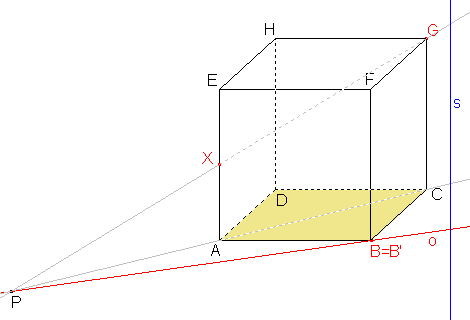 Pomocí bodů B, P již můžeme sestrojit osu afinity o. |
|
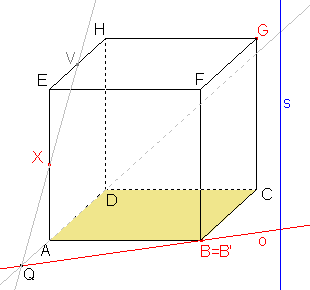 Sestrojíme bod řezu V na hraně krychle EH. Bod Q je průsečík přímky AD s osou o. Vzorem přímky AD v afinitě je přímka XQ a tedy bod řezu V je průsečíkem přímky XQ s hranou EH. |
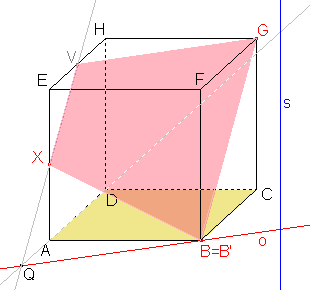 Nyní známe všechny vrcholy mnohoúhelníku, který je řezem, a strany tohoto mnohoúhelníku jsou hranicemi řezu v příslušných stěnách. |
Postup si ukážeme po krocích.
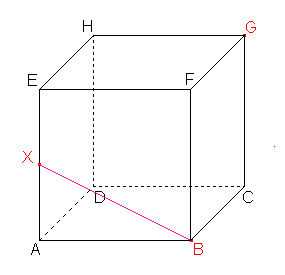 Dle důsledku 1: Body B, X roviny řezu leží v rovině přední stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je jednou stranou řezu. |
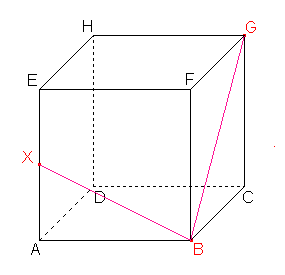 Dle důsledku 1: Body B, G roviny řezu leží v rovině pravé boční stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu. |
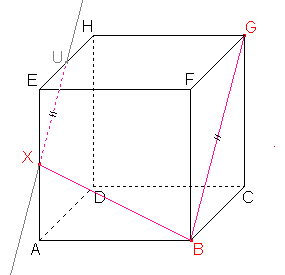 Sestrojíme bod U a stranu řezu XU v boční stěně ADE dle důsledku 2: Roviny bočních stěn jsou rovnoběžné a přitom různoběžné s rovinou řezu, proto jsou průsečnice roviny řezu s rovinami těchto stěn rovnoběžné. Můžeme tedy sestrojit rovnoběžku ke straně řezu BG procházející bodem X. Průnik rovnoběžky a hrany EH je hledaný bod U a úsečka XU je stranou řezu. |
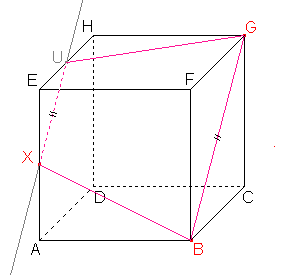 Dle důsledku 1: Body G, U roviny řezu leží v rovině horní stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu. |
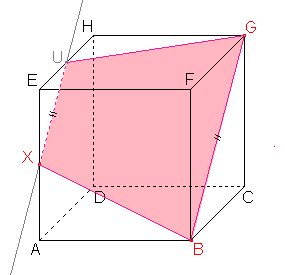 Nyní známe všechny vrcholy a strany mnohoúhelníku, který je řezem daného tělesa. |
Příklad 2
Sestrojte řez kosého čtyřbokého hranolu ABCDEFGH, jehož podstava je lichoběžník, rovinou XYZ, kde bod X leží na hraně DH, bod Y leží na hraně GH, bod Z leží na hraně BF.
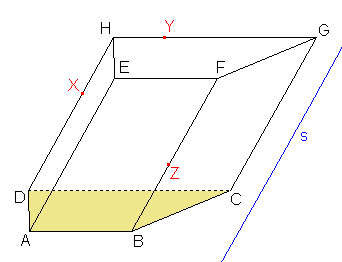
Řešení
Ukážeme si dva způsoby řešení - nejdříve pomocí osové afinity mezi rovinami a dále pomocí stereometrických vět a jejich důsledků.
a) Využijeme osové afinity mezi dvěma rovinami, a to rovinou řezu a rovinou dolní podstavy, za směr afinity s vezmeme směr bočních hran.
Postup si ukážeme po krocích.
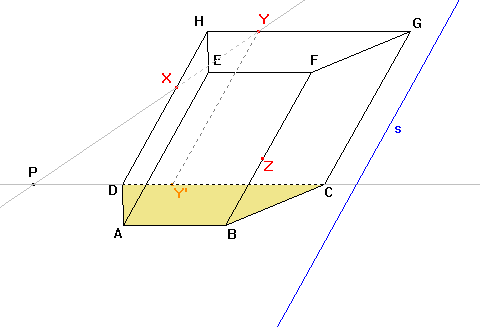 Nejprve musíme najít osu afinity, která je průsečnicí roviny dolní podstavy a roviny řezu dané body XYZ. K sestrojení osy afinity budeme potřebovat dva body. Jeden bod získáme pomocí bodů X, Y. Obrazem přímky XY je přímka DY', protože obrazem bodu X je bod D a bodu Y je bod Y'. Průsečíkem přímky XY a přímky DY' je samodružný bod P, který bude ležet na ose afinity. |
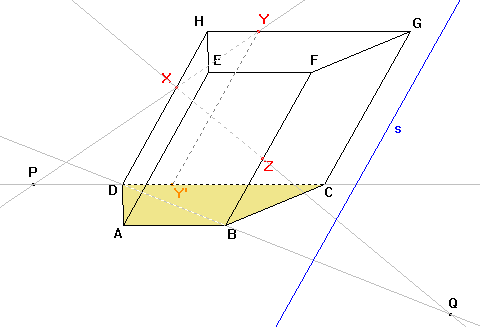 Druhý bod osy získáme pomocí bodů X, Z. Obrazem přímky XZ je přímka DB, protože obrazem bodu X je bod D a bodu Z je bod B. Průsečíkem přímky XZ a přímky DB je samodružný bod Q, který bude ležet na ose afinity. |
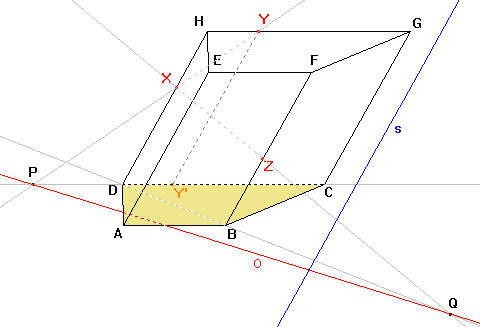 Pomocí bodů P, Q již můžeme sestrojit osu afinity o. |
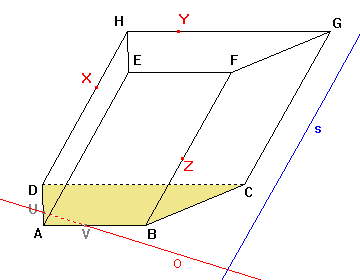 Osa afinity leží v rovině dolní podstavy tělesa a navíc protíná hrany podstavy, proto průsečíky U, V osy afinity s hranami dolní podstavy jsou body řezu. |
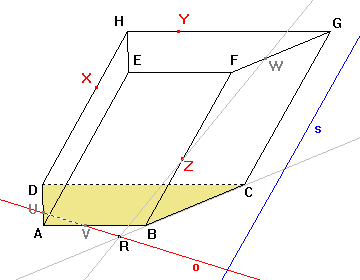 Sestrojíme bod řezu W na hraně FG. Bod R je průsečík přímky BC s osou o. Vzorem přímky BC je přímka ZR a tedy průsečík přímky ZR s hranou FG je bod řezu W. |
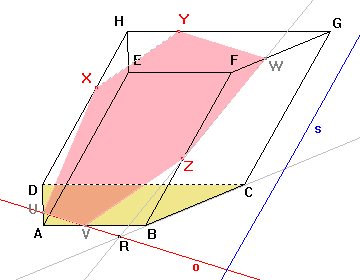 Nyní známe všechny vrcholy mnohoúhelníku, který je řezem, a strany tohoto mnohoúhelníku jsou hranicemi řezu v příslušných stěnách. |
Postup si ukážeme po krocích.
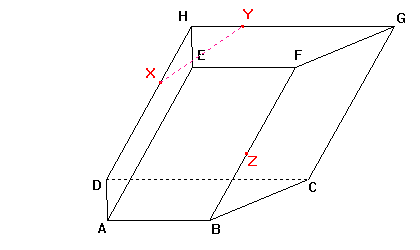 Dle důsledku 1: Body X, Y roviny řezu leží v rovině zadní stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je stranou řezu. |
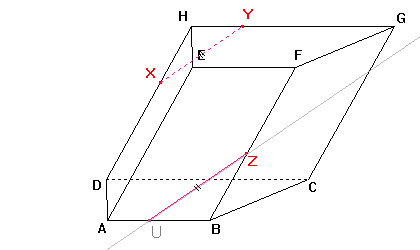 Sestrojíme bod U a stranu řezu ZU v přední stěně ABF dle důsledku 2: Roviny přední a zadní stěny jsou rovnoběžné a přitom různoběžné s rovinou řezu, proto jsou průsečnice roviny řezu s rovinami těchto stěn rovnoběžné. Můžeme tedy sestrojit rovnoběžku ke straně řezu XY procházející bodem Z. Průsečík rovnoběžky a hrany AB je hledaný bod U a úsečka ZU je stranou řezu. |
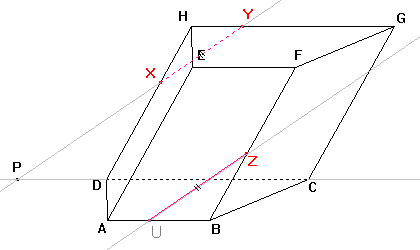 Dle důsledku 3 se průsečnice rovin zadní stěny a dolní podstavy, které jsou sousední, s rovinou řezu a přímka, v níž leží společná hrana těchto stěn, protínají v jednom bodě. Sestrojíme tedy přímku danou body CD, v níž leží společná hrana zadní stěny a dolní podstavy, a průsečnici roviny řezu a zadní stěny, kterou je přímka XY. Bod P je průsečíkem přímky CD a přímky XY. |
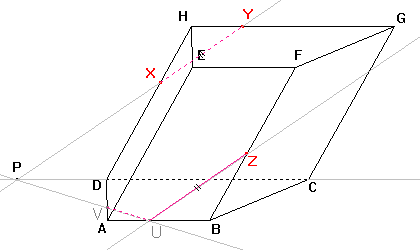 Dle důsledku 3 je bod P průsečíkem přímek CD, XY a přímky PU, která je průsečnicí roviny řezu a dolní podstavy. Nyní můžeme sestrojit průsečík V přímky PU a hrany AD a stranu řezu UV. |
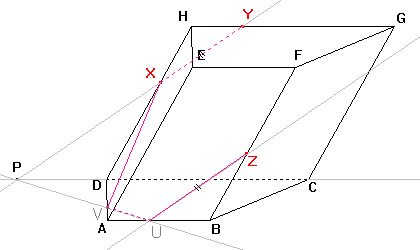 Dle důsledku 1: Body X, V roviny řezu leží v rovině boční stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu. |
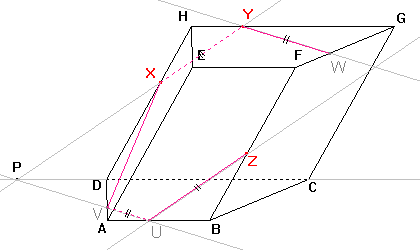 Sestrojíme bod W a stranu řezu YW v horní podstavě EFG dle důsledku 2: Roviny dolní a horní podstavy jsou rovnoběžné a přitom různoběžné s rovinou řezu, proto jsou průsečnice roviny řezu s rovinami podstav rovnoběžné. Můžeme tedy sestrojit rovnoběžku ke straně řezu UV procházející bodem Y. Průsečík rovnoběžky a hrany FG je hledaný bod W a úsečka YW je stranou řezu. |
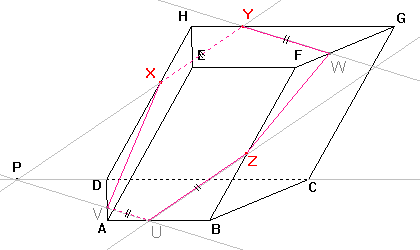 Dle důsledku 1: Body Z, W roviny řezu leží v rovině boční stěny, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu. |
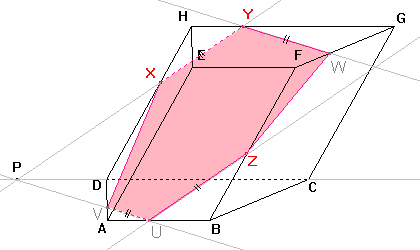 Nyní známe všechny vrcholy a strany mnohoúhelníku, který je řezem daného tělesa. |
Úlohy
1. Sestrojte řez krychle ABCDEFGH rovinou XYZ, kde bod X leží na hraně AE, bod Y leží na hraně DH, bod Z leží na polopřímce EF za bodem F.
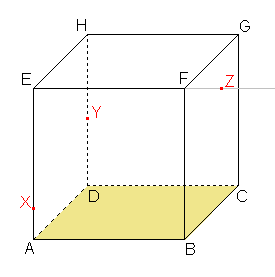
a) Řešte pomocí osové afinity. Řešení
b) Řešte pomocí stereometrických vět a jejich důsledků. Řešení
2. Sestrojte řez kvádru ABCDEFGH rovinou CXY, kde umístění bodů X, Y je dáno dělicím poměrem (AEX) = -1/3, (GHY) = -4.
a) Řešte pomocí osové afinity. Řešení
b) Řešte pomocí stereometrických vět a jejich důsledků. Řešení
3. Sestrojte řez kosého čtyřbokého hranolu ABCDEFGH, jehož podstavou je obdélník, rovinou XYZ, kde umístění bodů X, Y, Z je dáno dělicím poměrem (AEX) = -3/5, (CGY) = -7/3, (GHZ) = 4.
a) Řešte pomocí osové afinity. Řešení
b) Řešte pomocí stereometrických vět a jejich důsledků. Řešení
4. Sestrojte řez kolmého trojbokého hranolu ABCDEF rovinou XYZ, kde umistění bodů X, Y, Z je dáno dělicím poměrem (ADX) = -1/2, (EFY) = -3/2, (ABZ) = 4.
a) Řešte pomocí osové afinity. Řešení
b) Řešte pomocí stereometrických vět a jejich důsledků. Řešení
5. Sestrojte řez kosého trojbokého hranolu ABCDEF rovinou XYZ, kde umístění bodů X, Y, Z je dáno dělicím poměrem (BEX) = -1/3, (EFY) = -1, (EDZ) = 4.
a) Řešte pomocí osové afinity. Řešení
b) Řešte pomocí stereometrických vět a jejich důsledků. Řešení
6. Sestrojte řez kosého čtyřbokého hranolu ABCDEFGH, jehož podstavou je čtverec, rovinou XYZ, kde bod X leží na hraně AB, bod Y leží na hraně CG, bod Z leží na hraně EH.
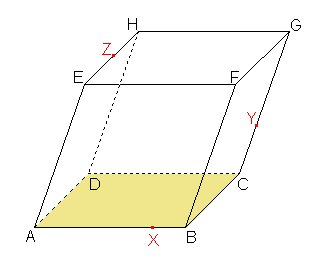
Řešení
7. Sestrojte řez pravidelného šestibokého hranolu ABCDEFGHIJKM rovinou XYZ, kde bod X leží na hraně FM, bod Y leží na hraně CI, bod Z leží na hraně JK.
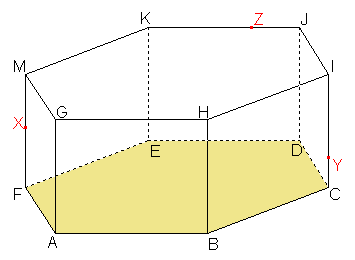
Řešení
8. Sestrojte řez kosého šestibokého hranolu ABCDEFGHIJKM, jehož podstavou je pravidelný šestiúhelník, rovinou XYZ, kde bod X leží na hraně AG, bod Y leží na hraně EK, bod Z leží na polopřímce HI za bodem I.
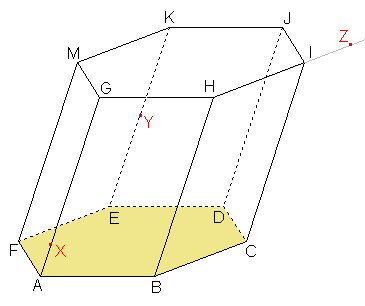
Řešení
9. Sestrojte řez kolmého pětibokého hranolu ABCDEFGHIJ rovinou XYZ, kde bod X leží na hraně AF, bod Y leží na hraně GH, bod Z leží na polopřímce ED za bodem D.
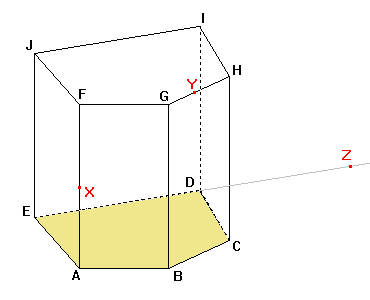
Řešení
10. Sestrojte řez kosého pětibokého hranolu ABCDEFGHIJ rovinou XYZ, kde bod X leží na hraně BG, bod Y leží na hraně DI, bod Z leží na polopřímce FJ za bodem J.
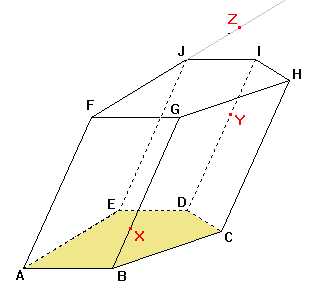
Řešení