Rovnoběžné promítání
Již malíři ve středověku se snažili zachytit nějakou skutečnost (přírodu, stavbu, životní styl) ve svých obrazech, neboli zobrazit nějaký prostorový útvar na rovinu (plátno). Jedna z možností, jak získat tento obraz, je použít rovnoběžné promítání. V dnešní době se toto zobrazení používá také pro stavební plány a technické nákresy.
Definice
Mějme rovinu α a přímku s, kterou budeme nazývat směr promítání, přičemž přímka s není rovnoběžná s rovinou α.
Rovnoběžné promítání prostoru na rovinu α směrem s je zobrazení, při kterém se body zobrazovaného vzoru promítají do roviny α vzájemně rovnoběžnými přímkami směru s.
Rovina α, na kterou zobrazujeme, se nazývá průmětna.
Obraz bodu nazýváme průmět bodu.
Přímka směru s, pomocí níž se zobrazuje bod do průmětny, se nazývá promítací přímka.
Promítací rovinou přímky p, p je různoběžná se směrem s, nazýváme rovinu, ve které leží přímka p a promítací přímky jejích bodů.
Rozlišujeme následující případy rovnoběžného promítání:
- pravoúhlé - s
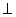 α
α - kosoúhlé - s
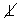 α
α
- Obrazem bodu je bod.
Není-li směr s rovnoběžný s průmětnou α, pak i promítací přímka libovolného bodu není rovnoběžná s průmětnou α. Průnikem promítací přímky s rovinou, jež jsou navzájem různoběžné, je jeden bod.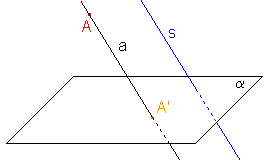
α...průmětna
s...směr promítání
a...promítací přímka bodu A
A'...průmět bodu A - Obrazem přímky p je:
a) bod p', jestliže p 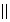 s,
s,b) přímka p', jestliže p  s.
s.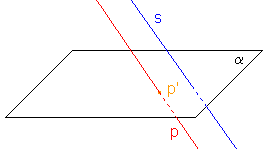
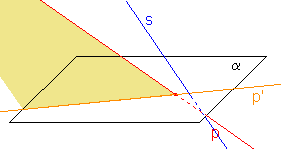
Všechny body přímky p se zobrazí do jednoho bodu p', protože jejich promítací přímky jsou totožné s přímkou p. Obrazem přímky p je průnik její promítací roviny a průmětny; průnikem dvou různoběžných rovin je přímka.
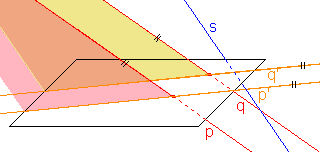
- Obrazem různých rovnoběžek p, q jsou:
a) dva různé body p', q', jestliže p  s,
s,b) rovnoběžky p', q', jestliže p 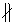 s.
s.
Je-li p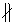 s, pak i q
s, pak i q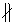 s a promítací roviny přímek p a q jsou rovnoběžné.
s a promítací roviny přímek p a q jsou rovnoběžné.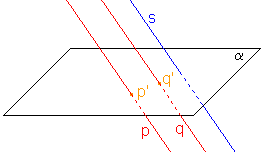
- Obrazem různoběžek p, q jsou:
a) různoběžky, nebo splývající rovnoběžky, jestliže p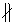 s a zároveň q
s a zároveň q 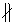 s;
s;
splývající rovnoběžky jsou to v případě, když promítací roviny přímek p, q splývají, tj. p, q leží v jedné promítací rovině,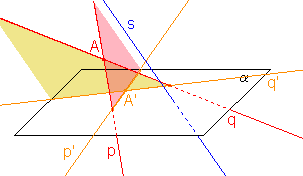
b) přímka q' a bod p', jestliže p  s a zároveň q
s a zároveň q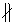 s; přímka q' prochází bodem p'.
s; přímka q' prochází bodem p'.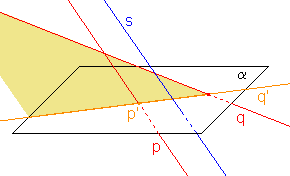
- Obrazem mimoběžek p, q jsou:
a) různoběžky, nebo různé rovnoběžky, jestliže p s a zároveň q
s a zároveň q  s;
s;
různé rovnoběžky jsou to v případě, když promítací roviny zadaných přímek jsou navzájem rovnoběžné,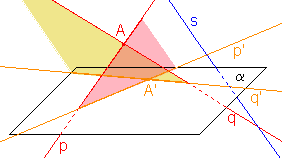
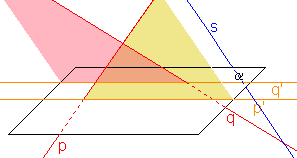
b) přímka q' a bod p', jestliže p  s a zároveň q
s a zároveň q s, a přímka q' neprochází bodem p'
s, a přímka q' neprochází bodem p'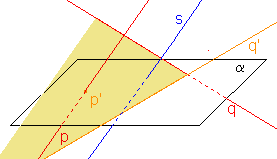
- Obrazem roviny β je:
a) průmětna α, jestliže β  s,
s,b) přímka b, jestliže β 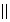 s
s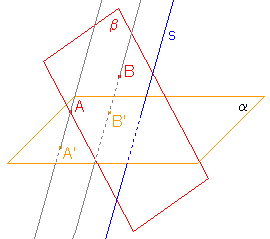
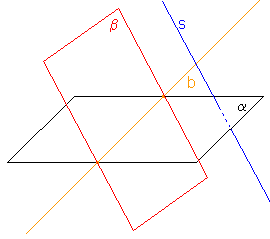
Je-li β 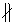 s, pak promítací přímky bodů roviny β nejsou rovnoběžné s průmětnou α. Obrazy bodů roviny β jsou body roviny α.
s, pak promítací přímky bodů roviny β nejsou rovnoběžné s průmětnou α. Obrazy bodů roviny β jsou body roviny α.Je-li β 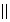 s, pak průsečnice roviny β s rovinou α je obrazem roviny β.
s, pak průsečnice roviny β s rovinou α je obrazem roviny β. - Obrazem konvexního n-úhelníku (n
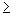 3, n
3, n 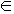 N) ležícího v rovině β a s vrcholy
N) ležícího v rovině β a s vrcholy 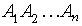 je:
je:
a) opět konvexní n-úhelník s vrcholy 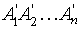 ,přičemž
,přičemž 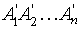 jsou po řadě rovnoběžné průměty vrcholů
jsou po řadě rovnoběžné průměty vrcholů 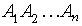 , je-li β
, je-li β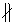 s.
s.b) úsečka, je-li β 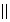 s.
s.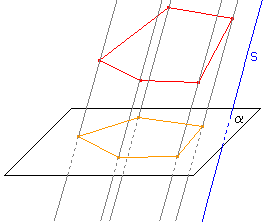
- Incidence se zachovává (např. je-li B
 p, pak B'
p, pak B' 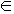 p').
p'). - Dělicí poměr se zachovává (je-li (ABC)=λ, pak (A'B'C')=λ).
- Obrazy útvarů ležících v rovině rovnoběžné s průmětnou jsou shodné se svými vzory.