Podstavy těles
Než se pustíme do složitějších úloh jako jsou řezy těles, měli bychom se seznámit s tím, jak tato tělesa rovnoběžně promítnout do roviny. My se zde budeme zabývat pouze hranoly a válci. Tato tělesa mají dolní podstavu shodnou s horní podstavou, a tedy k zobrazení těchto těles nám stačí prozkoumat, jak se promítne například dolní podstava daného tělesa.
Ukážeme si dva způsoby, jak získat průmět podstavy tělesa do roviny. V prvním z nich využijeme osovou afinitu v rovině a ve druhém volné rovnoběžné promítání.
Volné rovnoběžné promítání je druh rovnoběžného promítání, je zde určitá volnost ve volbě směru s.
Většina obrázků v učebnicích stereometrie je sestrojena v tomto promítání.
Poznámky k použití volného rovnoběžného promítání
- Průmětnu volíme svislou (např. obrazovka počítače, rovina tabule).
- Podstavy těles umisťujeme do vodorovných rovin tak, aby některá podstavná hrana byla rovnoběžná s průmětnou (u hranolů).
- Úsečky kolmé k průmětně zobrazujeme jako přímky zpravidla s odchylkou 45° od vodorovného směru a vzdálenosti na nich zkracujeme na polovinu.
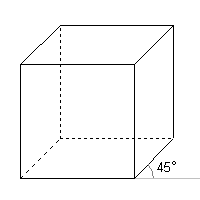
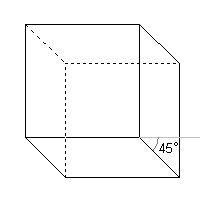
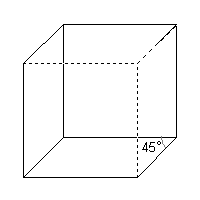
Přední stěnu krychle umístíme do roviny rovnoběžné s průmětnou, zobrazí se tedy ve skutečné velikosti, a dále:
- je-li vidět horní podstavu a pravou boční stěnu, nazývá se tento pohled nadhled zprava
- je-li vidět horní podstavu a levou boční stěnu, nazývá se tento pohled nadhled zleva
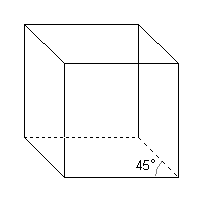
- je-li vidět dolní podstavu a pravou boční stěnu, nazývá se tento pohled podhled zprava
- je-li vidět dolní podstavu a levou boční stěnu, nazývá se podhled zleva
 |  |  |  |
Příklad
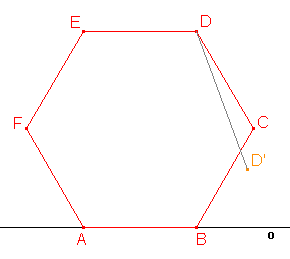
Je dáno těleso, jehož podstavou je obecný pětiúhelník. Najděte obraz podstavy v rovnoběžném promítání použitím:
a) osové afinity určené osou o a uspořádanou dvojicí bodů DD',
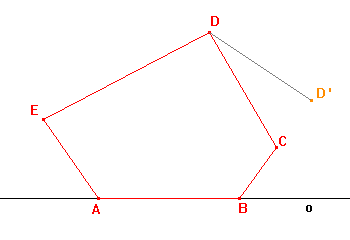
b) volného rovnoběžného promítaní.
Řešení
Postupy si ukážeme po krocích.
a)
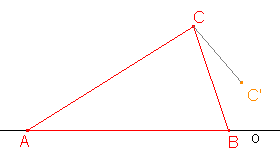
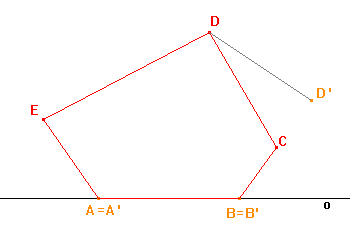 Abychom mohli najít obraz daného pětiúhelníku, musíme najít obrazy jeho vrcholů. Všimněme si, že pětiúhelník ABCDE má s osou o společnou jednu celou stranu, tj. na ose o leží body A, B, které jsou samodružné. Již máme body A', B' a D' (bod D' je dán ze zadání), stačí nalézt obrazy bodů C, E. |
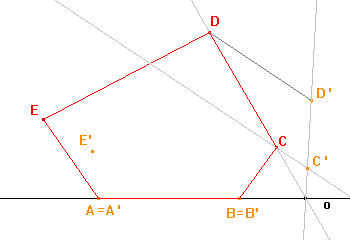 Sestrojíme obraz C' bodu C a obdobným postupem obraz E' bodu E, a to stejně jako v Příkladu 1a v kapitole o osové afinitě v rovině. |
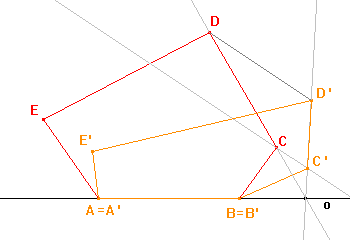 Pomocí bodů A', B', C', D', E' načrtneme obraz pětiúhelníku ABCDE, kterým bude pětiúhelník A'B'C'D'E'. |
b)
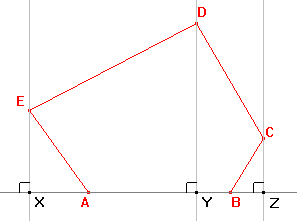 Podstavu tělesa umístíme do vodorovné roviny tak, aby hrana AB byla rovnoběžná s průmětnou. Abychom mohli najít obraz daného pětiúhelníku, musíme najít obrazy jeho vrcholů. Nejprve spustíme kolmice z bodů E, D, C na přímku AB. Paty kolmice označíme X, Y, Z. |
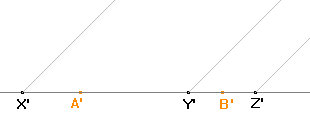 Platí |AB|=|A'B'|, |YX|=|Y'X'|, |BZ|=|B'Z'|, protože přímka AB je rovnoběžná s průmětnou a rovnoběžné promítání zobrazuje útvary ležící v rovnoběžné rovině s průmětnou na shodný útvar. Polopřímky XE, YD, ZC se zobrazí na polopřímky X'E', Y'D' , Z'C', které mají s přímkou AB odchylku 45°. |
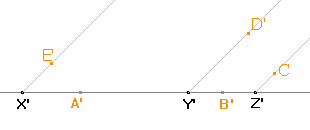 Na polopřímku s počátečním bodem X' naneseme od počátku poloviční délku úsečky XE a tak získáme bod E'. Obdobně nalezneme bod D' a C'. |
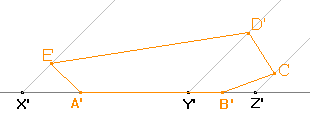 Pomocí bodů A', B', C', D', E' načrtneme obraz pětiúhelníku ABCDE, kterým bude pětiúhelník A'B'C'D'E'. |
Úlohy
- 1. Je dáno těleso, jehož podstavou je čtverec ABCD. Najděte obraz podstavy v rovnoběžném promítání použitím:
- a) osové afinity určené osou o a uspořádanou dvojicí bodů DD',
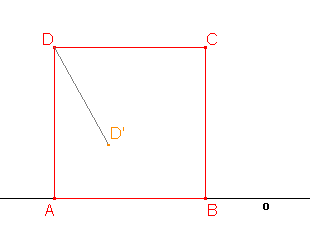
Řešení - b) volného rovnoběžného promítaní.
Řešení
- 2. Je dáno těleso, jehož podstavou je kruh k. Najděte obraz podstavy v rovnoběžném promítání použitím:
- a) osové afinity určené osou o a uspořádanou dvojicí bodů SS',
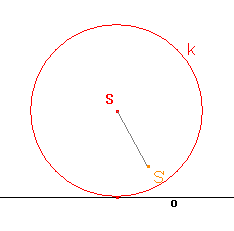
Řešení - b) volného rovnoběžného promítaní.
Řešení