Úloha 3b
| zobraz celé řešení | |
| << předchozí snímek | následující snímek >> |
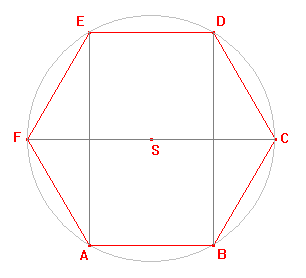 |
Zadání: Je dáno těleso, jehož podstavou je pravidelný šestiúhelník ABCDE. Najděte obraz podstavy použitím volného rovnoběžného promítaní.
Podstavu tělesa umístíme do vodorovné roviny tak, aby podstavná hrana AB byla rovnoběžná s průmětnou.
Abychom mohli najít obraz daného šestiúhelníku, musíme najít obrazy jeho vrcholů. Všimněme si, že body ABDE tvoří obdélník a ten můžeme sestrojit obdobně jako čtverec v Úloze 1b. Tím získáme body D', E'.
Rovnoběžné promítání zachovává dělící poměr a proto obraz středu S, který půlí úhlopříčky obdélníku ABDE, je střed S', který půlí úhlopříčky rovnoběžníku A'B'D'E'.
Platí |FS|=|F'S'|, |CS|=|C'S'|, protože přímka FC je rovnoběžná s průmětnou a rovnoběžné promítání zobrazuje útvary ležící v rovnoběžné rovině s průmětnou na shodné útvary. Tohoto můžeme využít při konstrukci bodů C', F'.
Pomocí bodů A', B', C', D', E', F' načrtneme obraz pravidelného šestiúhelníku ABCDEF, kterým bude šestiúhelník A'B'C'D'E'F'.
|
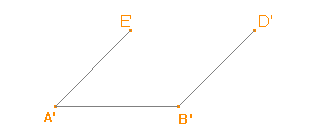 |
Podstavu tělesa umístíme do vodorovné roviny tak,aby podstavná hrana AB byla rovnoběžná s průmětnou. Abychom mohli najít obraz daného šestiúhelníku, musíme najít obrazy jeho vrcholů. Všimněme si, že body ABDE tvoří obdélník a ten můžeme sestrojit obdobně jako čtverec v Úloze 1b. Tím získáme body D', E'. |
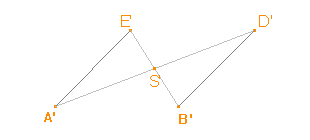 |
Rovnoběžné promítání zachovává dělící poměr a proto obraz středu S, který půlí úhlopříčky obdélníku ABDE, je střed S', který půlí úhlopříčky rovnoběžníku A'B'D'E'. |
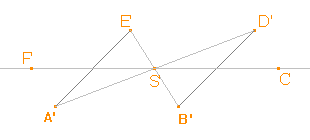 |
Platí |FS|=|F'S'|, |CS|=|C'S'|, protože přímka FC je rovnoběžná s průmětnou a rovnoběžné promítání zobrazuje útvary ležící v rovnoběžné rovině s průmětnou na shodné útvary. Tohoto můžeme využít při konstrukci bodů C', F'. |
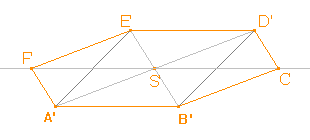 |
Pomocí bodů A', B', C', D', E', F' načrtneme obraz pravidelného šestiúhelníku ABCDEF, kterým bude šestiúhelník A'B'C'D'E'F'. |