Úloha 4b
| zobraz celé řešení | |
| << předchozí snímek | následující snímek >> |
 |
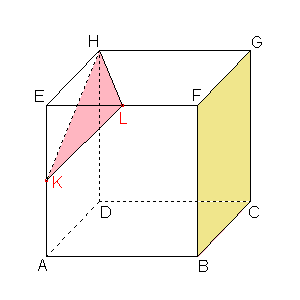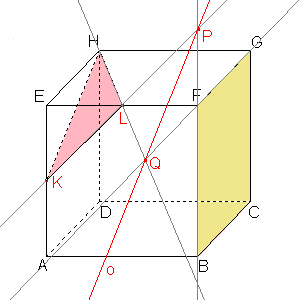
Zadání: Je dána krychle ABCDEFGH a roviny α=  BCG a β= KLH, kde K je střed hrany AE a L je střed hrany EF.Najděte osu afinity mezi rovinami α a β. Směr afinity budeme brát kolmý k rovině α, obrazem bodu F je bod L.
Obrazem přímky dané body KL je přímka BF.
Průsečíkem přímky BF a přímky KL je samodružný bod P, který bude ležet na ose afinity.
Sestrojíme průsečík Q přímky HL a jejího obrazu.
Osa afinity prochází samodružnými body P, Q.
|
zobraz řešení interaktivně
 |
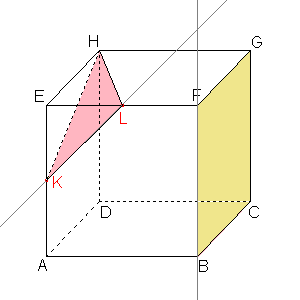Obrazem přímky dané body KL je přímka BF. |
 |
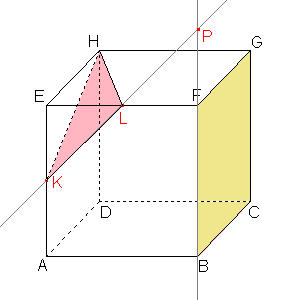Průsečíkem přímky BF a přímky KL je samodružný bod P, který bude ležet na ose afinity. |
 |
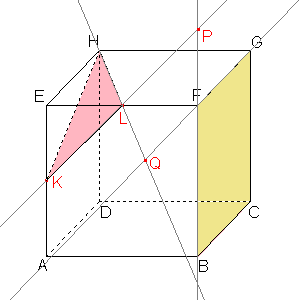Sestrojíme průsečík Q přímky HL a jejího obrazu. |
 |
Osa afinity prochází samodružnými body P, Q. |