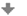Hyperbolické funkcie
Definice
Funkcia {\rm sinh}\: x (čítame hyperbolický sínus), {\rm cosh}\: x (čítame hyperbolický kosínus), {\rm tgh}\: x (čítame hyperbolický tangens) sú pre každé reálne x definované takto:
\sinh x = \frac {\large e^x - \large e^{-x}}{2}, \quad \cosh x = \frac {\large e^x + \large e^{-x}}{2}, \quad {\rm tgh}\: x = \frac {\large e^x - \large e^{-x}}{\large e^x + \large e^{-x}} = \large\frac {\sinh x} {\cosh x}.
Pre x \neq 0 je funkcia {\rm cotgh}\: x (čítame hyperbolický kotangens) definovaná vzťahom{\rm cotgh}\: x = \frac {\large e^x + \large e^{-x}}{\large e^x - \large e^{-x}} = \large\frac {1} {{\rm tgh}\: x}.
Základné vlastnosti hyperbolických funkcií
V tabuľke je uvedený prehľad základných vlastnosti hyperbolických funkcií.
|
Hyperbolická funkcia |
{\rm sinh}\: x |
{\rm cosh}\: x |
{\rm tgh}\: x |
{\rm cotgh}\: x |
|
Definičný obor |
\mathbb{R} |
\mathbb{R} |
\mathbb{R} |
(-\infty, 0)\cup (0, \infty) |
|
Obor funkčných hodnôt |
\mathbb{R} |
\left \langle 1, \infty \right) |
(-1, 1) |
(-\infty, -1)\cup (1, \infty) |
|
Monotónnosť |
rastúca na celom \mathbb{R} |
rastúca na intervale \left \langle 0, \infty \right) a klesajúca na intervale \left (-\infty, 0 \right \rangle |
rastúca na celom \mathbb{R} |
klesajúca na intervale(-\infty, 0)\cup (0, \infty) |
Veta
Pre hyperbolické funkcie platí:
1. \sinh\ x, {\rm cotgh}\: x a {\rm tgh}\: x sú nepárne funkcie.
2. {\rm cosh}\: x je párna funkcia.
Poznámka
V dôkaze týchto viet využívame vlastnosť párnej funkcie:
f(x) = f(-x),alebo nepárnej funkcie:
f(-x) = -f(-x).Grafy hyperbolických funkcií a ďalších funkcií
Poznámka
Grafy hyperbolických funkcií sú vytvorené pomocou programu GeoGebra, kde sa používa iné značenie hyperbolických funkcií. Preto napríklad funkcia {\rm tgh}\: x sa v GeoGebre značí ako {\rm tanh}\: x.Hyperbolický sínus
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie hyperbolický sínus.
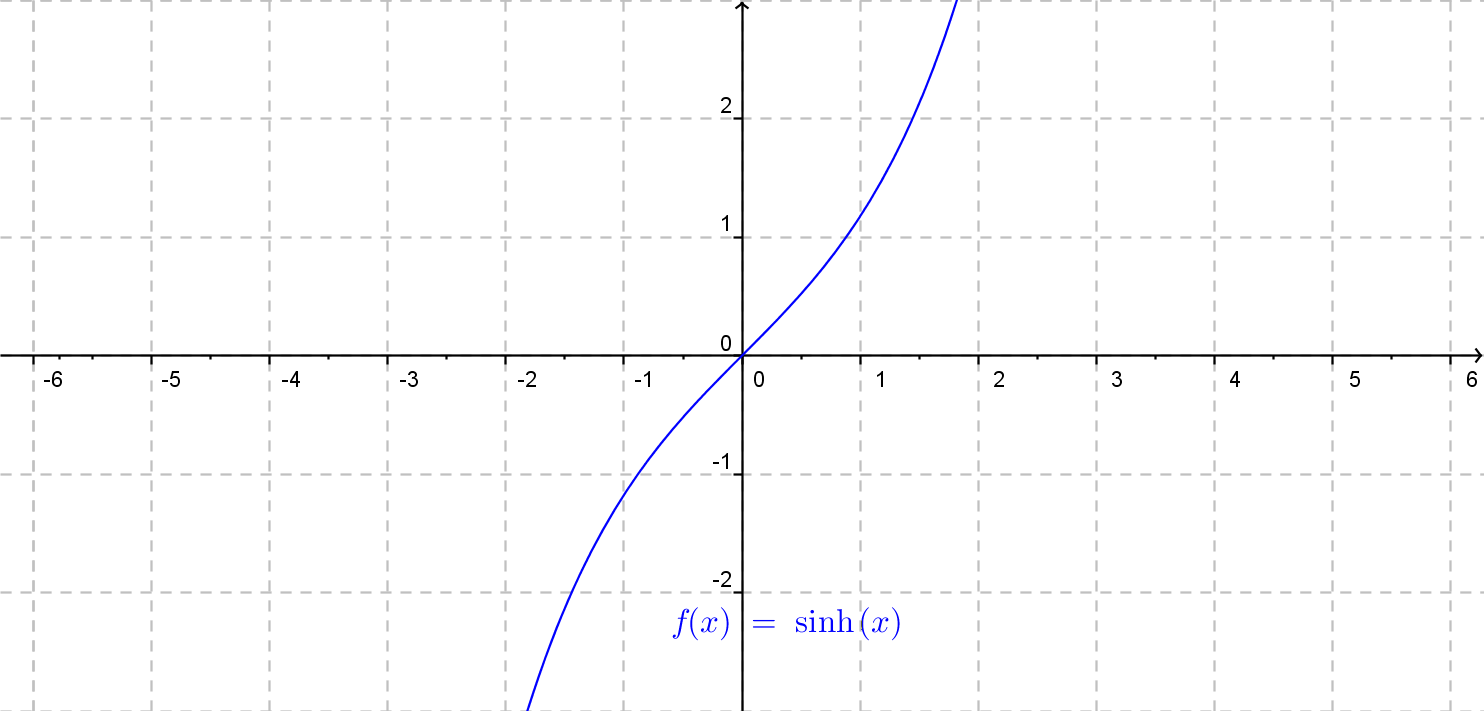
Funkcia f(x)= a \cdot {\rm sinh}\: x (b\cdot x + c) + d.
Poznámka
Grafy funkcií sú zobrazované pomocou apletu. V jednotlivých apletoch je možné pomocou posuvníkov meniť základné hodnoty parametrov a,b,c,d a všimnuť si tak správanie funkcií pri rôznych zmenách.
V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
Hyperbolický kosínus
Obecný graf funkcie hyperbolický kosínus.
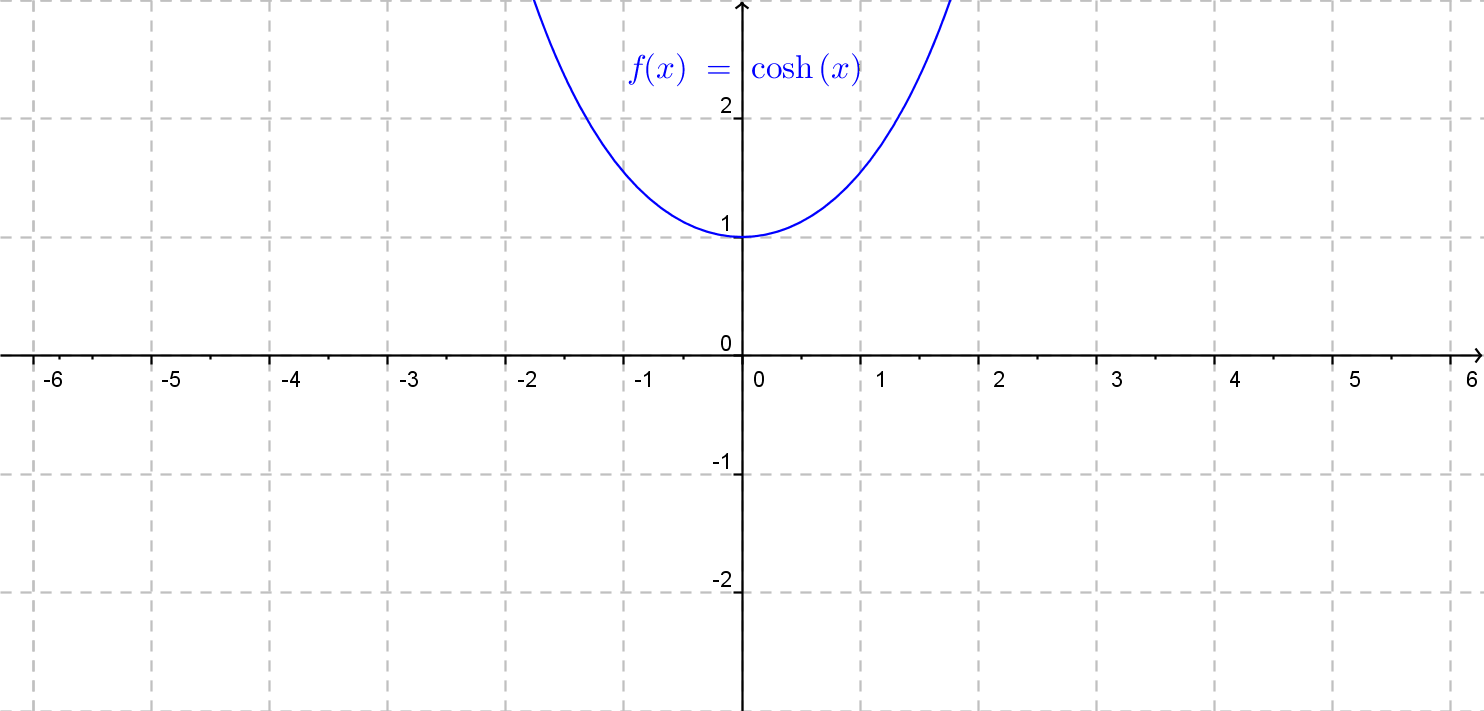
Funkcia f(x)= a \cdot {\rm cosh}\: x (b\cdot x + c) + d.
V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
Hyperbolický tangens
Obecný graf funkcie hyperbolický tangens.
Funkcia f(x)= a \cdot {\rm tgh}\: x (b\cdot x + c) + d.
V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
Hyperbolický kotangens
Obecný graf funkcie hyperbolický kotangens.
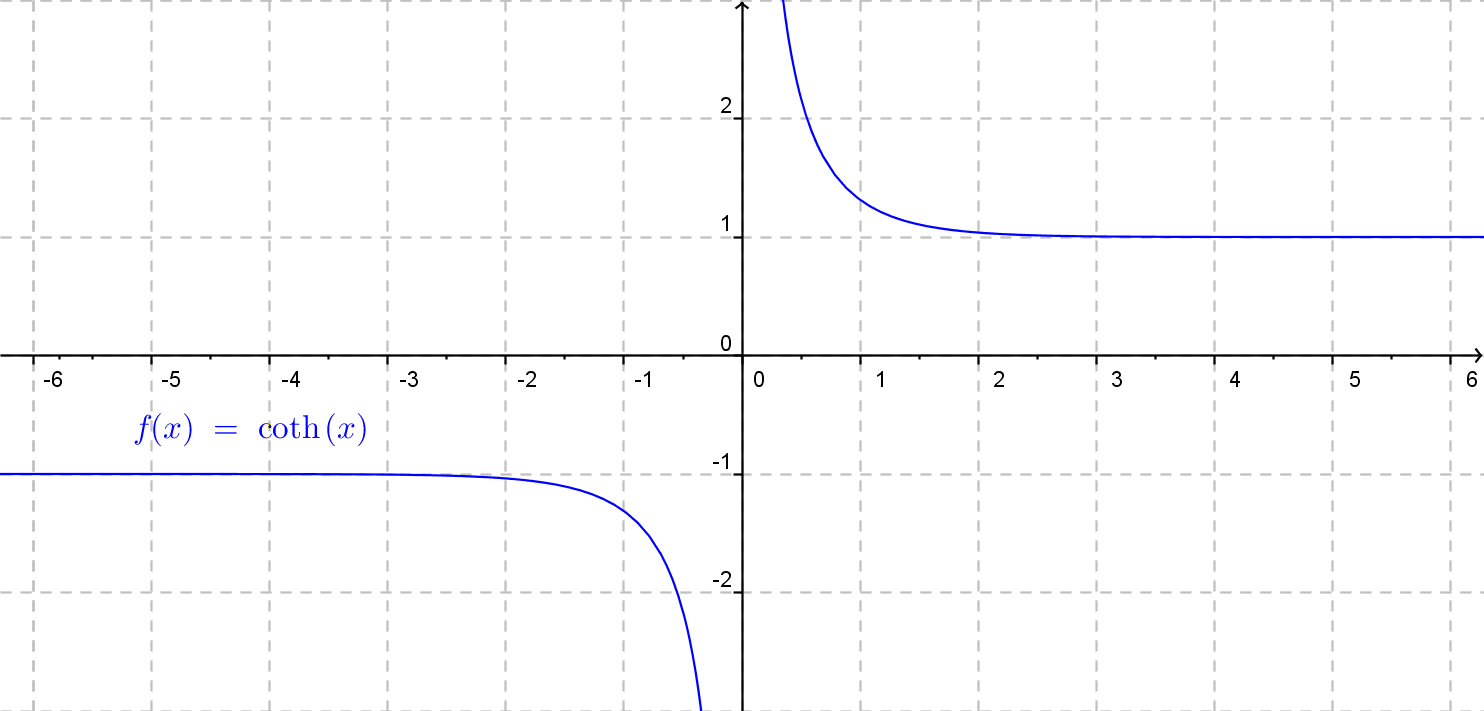
Funkcia f(x)= a \cdot {\rm cotgh}\: x (b\cdot x + c) + d.
V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
Veta
Pre hyperbolické funkcie platí:
\cosh^2 x - \sinh^2 x = 1 \ (x \in \mathbb{R}),
1 - {\rm tgh^2}\: x = \frac {\Large 1}{\Large {\rm cosh^2}\: x} (x \in \mathbb{R}) ,
{\rm cotgh^2}\: x - 1 = \frac {\Large 1}{\Large{\rm sinh^2}\: x}\ (x \not = 0).
Poznámka
Dôkaz tejto vety plynie zo základnej definicie hyperbolických funkcií. Postupnou úpravou dostávame požadované výsledky.
