Goniometrické funkcie
Základné vlastnosti goniometrických funkcií
V tabuľke je uvedený prehľad základných vlastnosti goniometrických funkcií, ktoré využívame pri riešeni príkladov. Hodnoty argumentov uvádzame väčšinou v oblúkovej miere.
|
Goniometrická funkcia |
\sin x |
\cos x |
{\rm tg}\: x |
{\rm cotg}\: x |
|
Definičný obor |
\mathbb{R} |
\mathbb{R} |
\bigcup\limits_{k\in\mathbb{Z}}\left ( -{\pi \over 2} + k\pi; {\pi \over 2} + k\pi \right ) |
\bigcup\limits_{k\in\mathbb{Z}}\left ( k\pi; (k+1)\pi \right ) |
|
Obor funkčných hodnôt |
\left \langle -1; 1 \right \rangle |
\left \langle -1; 1 \right \rangle |
\mathbb{R} |
\mathbb{R} |
|
Najmenšia perióda |
2\pi |
2\pi |
\pi |
\pi |
Grafy goniometrických a ďalších funkcií
Poznámka
Grafy funkcií sú zobrazené na intervale <-2\pi; 2\pi>.Sínus
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie sínus.
Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/teoria.goniometricke_funkcie.inc on line 111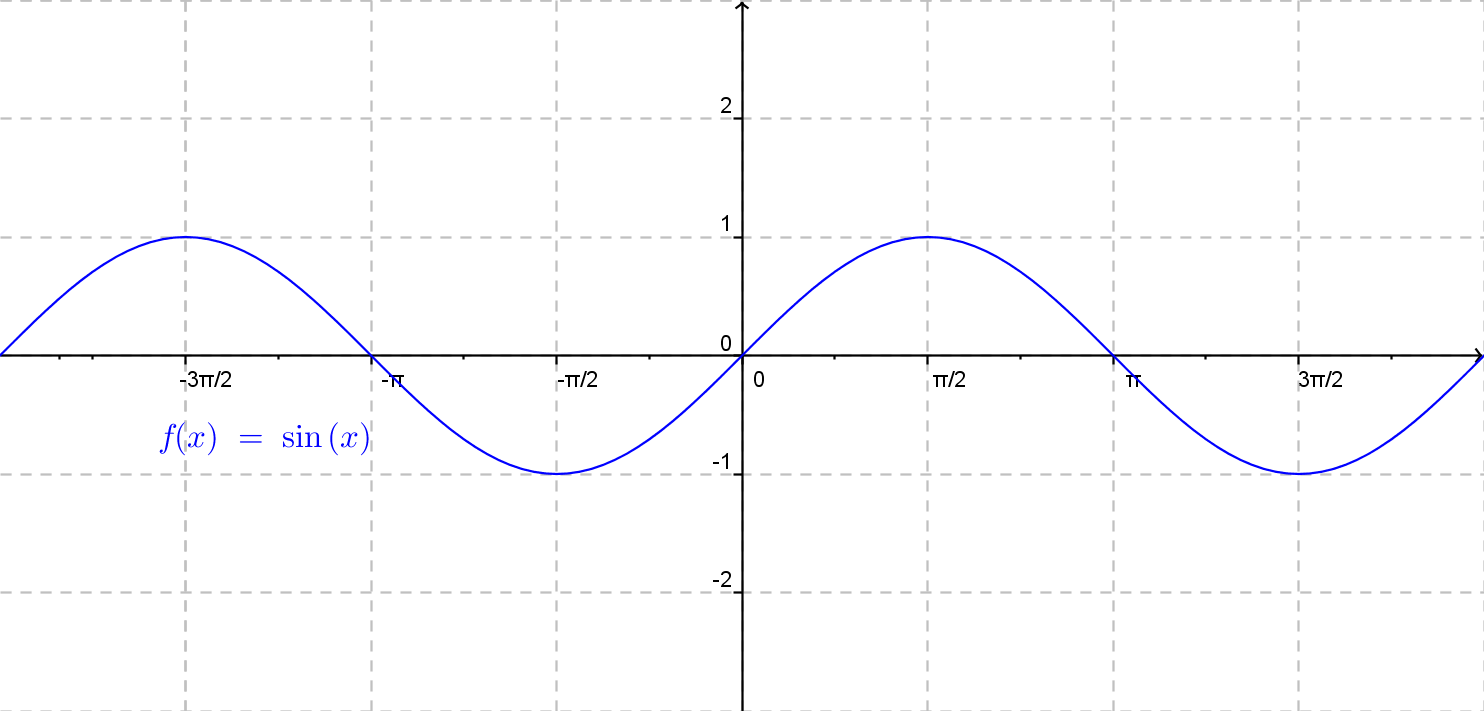
Graf funkcie y = \sin x nazývame sínusoida.
Zo sínusoidy môžme prečítať jej základné vlastnosti a porovnať ich tak s tabuľkou uvedenou na začiatku tejto kapitoly.
Funkcia f(x)= a \cdot \sin (b\cdot x + c) + d.
Takáto funkcia sa nazýva harmonická. V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
Je dôležité si všimnuť ako sa mení samotný graf pri rôznych zmenach parametrov.
Kosínus
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie kosínus.
Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/teoria.goniometricke_funkcie.inc on line 169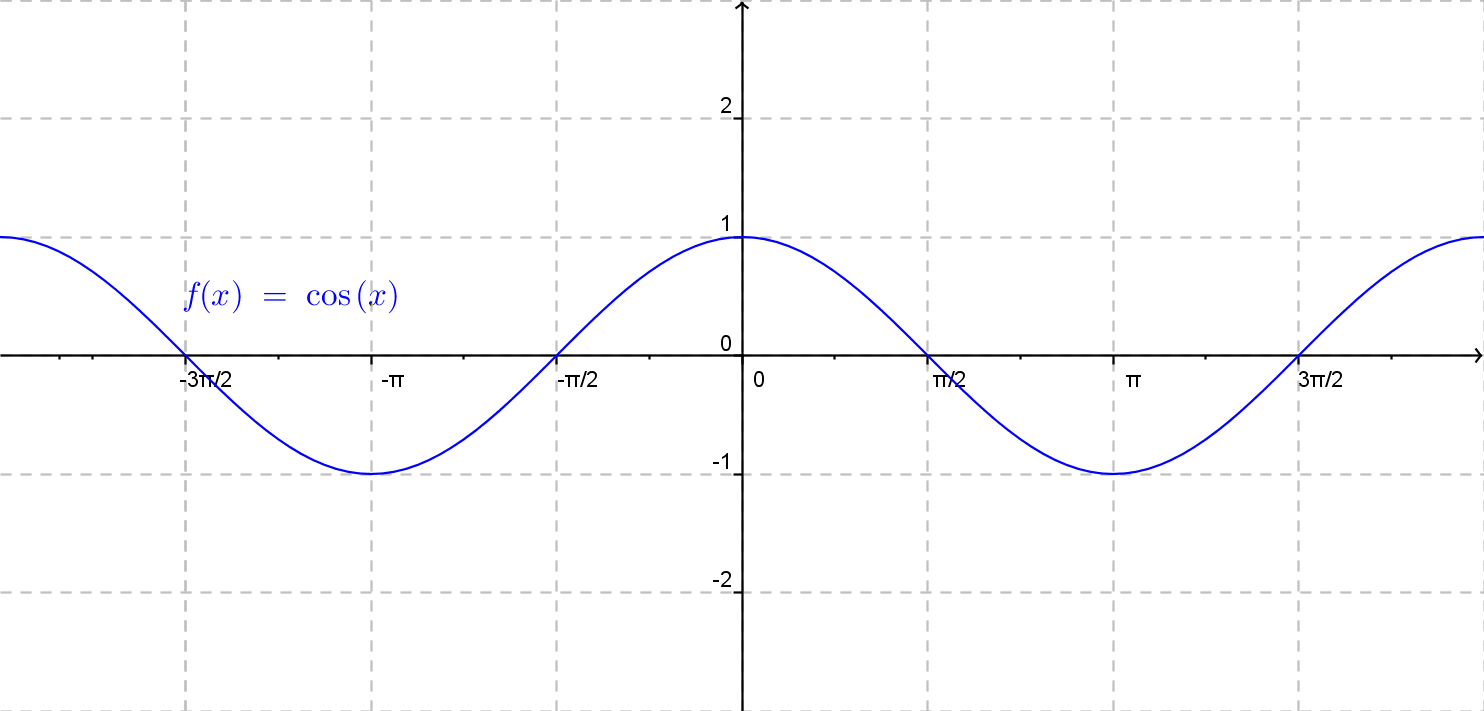
Graf funkcie y = \cos x nazývame kosínusoida.
Z kosínusoidy môžme prečítať základné vlastnosti funkcie kosínus a porovnať ich tak s tabuľkou uvedenou na začiatku tejto kapitoly.
Funkcia f(x)= a \cdot \cos (b\cdot x + c) + d.
Takáto funkcia sa nazýva harmonická. V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
Opäť je dôležité si všimnuť správanie grafu funkcie pri rôznych zmenach parametrov.
Tangens
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie tangens.
Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/teoria.goniometricke_funkcie.inc on line 225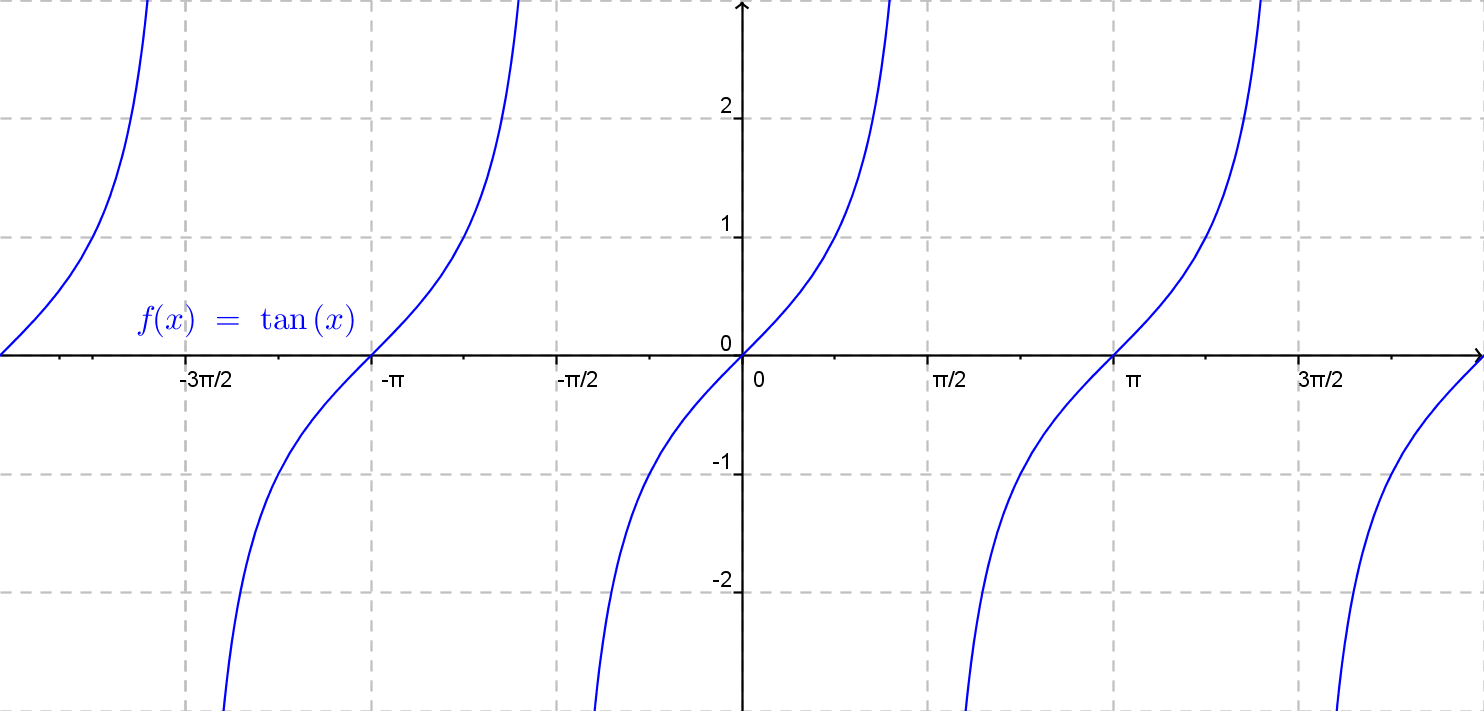
Funkcia f(x)= a \cdot {\rm tg}\: (b\cdot x + c) + d.
V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
V prípade, že parametre a = 1, b = 1, c = 0, d = 0 dostávame obecný graf funkcie tangens. Pri týchto apletoch je dôležité si všimnuť chovanie funkcie pri zmenách jednotlivých parametrov. Napríklad v špecialnom prípade, kde koeficient pri parametre b je nulový, dostávame konštantnú funkciu.Kotangens
Obecný graf funkcie kotangens je znázornený na nasledujúcom obrázku.
Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/teoria.goniometricke_funkcie.inc on line 285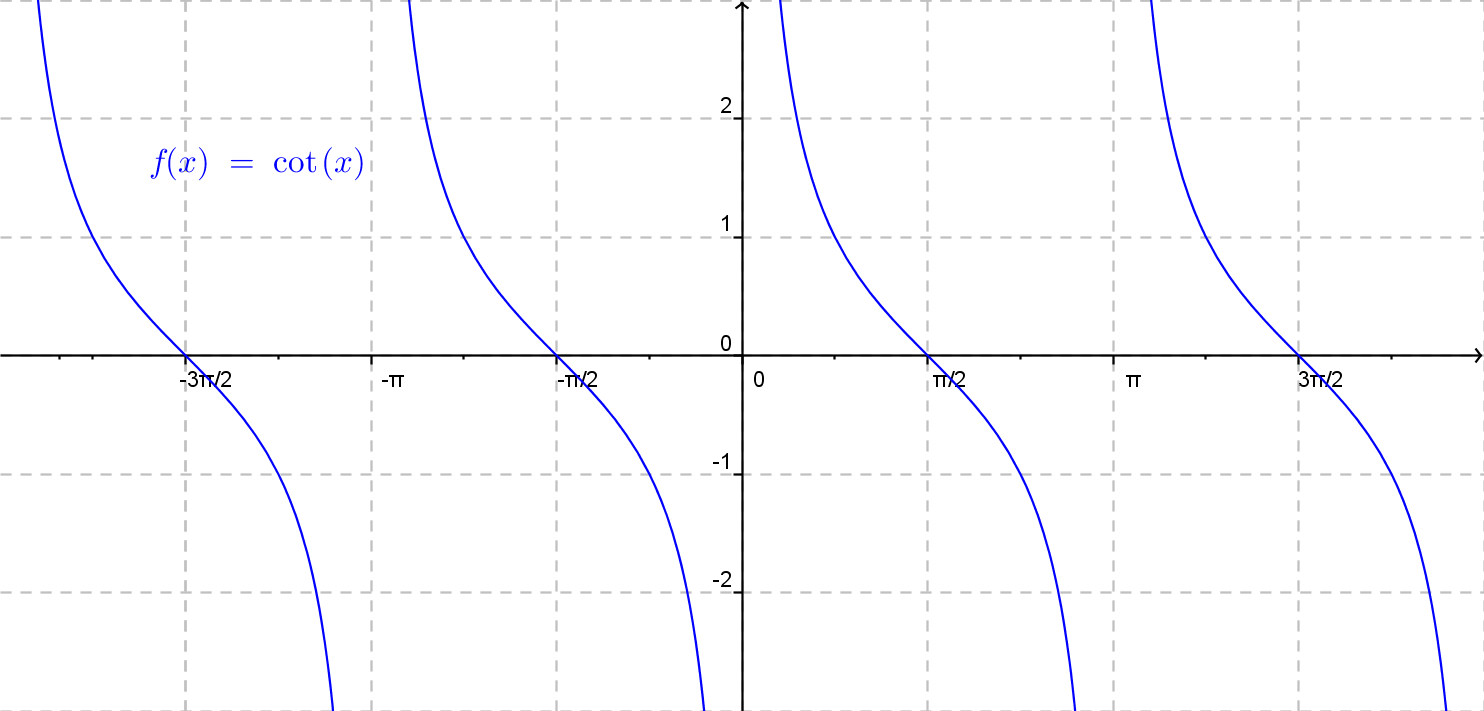
Funkcia f(x)= a \cdot {\rm cotg}\: (b\cdot x + c) + d.
V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
V prípade, že parametre a = 1, b = 1, c = 0, d = 0 dostávame obecný graf funkcie kotangens. Pri týchto apletoch je dôležité si všimnuť chovanie funkcie pri zmenách jednotlivých parametrov. Napríklad v špecialnom prípade, kde koeficient pri parametre b je nulový, dostávame konštantnú funkciu.Prehľad základných tabuľkových hodnôt
|
|
0 |
{\Large \pi \Large \over \large 6} |
{\Large \pi \Large \over \large 4} |
{\Large \pi \Large \over \large 3} |
{\Large \pi \Large \over \large 2} |
\pi |
{\Large 3\pi \Large \over \large 2} |
2\pi |
|
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
|
\sin x |
0 |
\Large {1 \over 2} |
\Large {\sqrt{2} \Large \over 2} |
\Large {\sqrt{3} \Large \over 2} |
1 |
0 |
-1 |
0 |
|
\cos x |
1 |
\Large {\sqrt{3} \Large \over 2} |
\Large {\sqrt{2} \Large \over 2} |
\Large {1 \over 2} |
0 |
-1 |
0 |
1 |
|
{\rm tg}\: x |
0 |
\Large {\sqrt{3} \Large \over 3} |
1 |
\sqrt{3} |
* |
0 |
* |
0 |
|
{\rm cotg}\: x |
* |
\sqrt{3} |
1 |
\Large {\sqrt{3} \Large \over 3} |
0 |
* |
0 |
* |
Poznámka
Symbol * znamená, že pre dané x nie je funkcia definovaná.