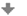Príklady
- Príklad 1
- Riešte goniometrickú nerovnicu s neznámou x \in \mathbb{R}:
\sin 2x \leq {1 \over 2}
Riešenie
Zavedieme pomocnú substitúciu y = 2x.
\sin y \leq {1 \over 2} Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/zloznerovnice.priklady.inc on line 12
Situáciu zobrazíme na jednotkovej kružnici:
Využitím jednotkovej kružnice dostávame riešenie:
y \in \left \langle {5 \over 6} \pi + 2k\pi; 2\pi + {\pi \over 6} + 2k\pi \right \rangle = \left \langle {5 \over 6}\pi + 2k\pi; {13 \over 6}\pi + 2k\pi \right \rangle
Vrátime sa k subtitúcií y = 2x, odkiaľ plynie, že 2x \in \left \langle {5 \over 6}\pi + 2k\pi; {13 \over 6}\pi + 2k\pi \right \rangle.
Úpravou dostávame x \in \left \langle {5 \over 12}\pi + k\pi; {13 \over 12}\pi + k\pi \right \rangle, k \in \mathbb{Z}.
Výsledné riešenie zapíšeme v tvare K = \bigcup\limits_{k\in\mathbb{Z}} \left \langle {5 \over 12}\pi + k\pi; {13 \over 12}\pi + k\pi \right \rangle.
- Príklad 2
- Riešte goniometrickú nerovnicu s neznámou x \in \mathbb{R}:
|{\rm tg}\: x| \geq {\rm tg}\: {\large \pi \over 3}
Riešenie
Aby výrazy v nerovnici boli definované, musí platiť podmienka x \not= (2k + 1){\large \pi \large \over \large 2}, k \in \mathbb{Z}.
|{\rm tg}\: x| \geq \sqrt {3} (Použili sme tabuľkovú hodnotu funkcie tangens uvedenú v časti.)
Z definície absolútnej hodnoty vyplýva:
{\rm tg}\: x \leq - \sqrt {3} \vee {\rm tg}\: x \geq \sqrt {3} Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/zloznerovnice.priklady.inc on line 32
(Bližšie informácie o absolútnej hodnote môžme nájsť v bakalárskej práci Základné poznatky z matematiky na strednej škole.)
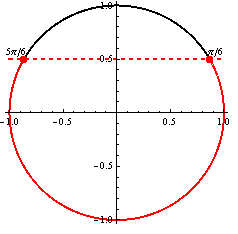
Využitím grafu funkcie a periodičnosti funkcie tangens dostávame riešenie:
x \in \left (-{\pi \over 2} + k\pi; -{\pi \over 3} + k\pi \right \rangle \cup \left \langle {\pi \over 3} + k\pi; {\pi \over 2} + k\pi \right ), k \in \mathbb{Z}.
Výsledné riešenie zapíšeme v tvare K = \bigcup\limits_{k\in\mathbb{Z}} \Big\{\left(-{\pi \over 2} + k\pi; -{\pi \over 3} + k\pi \right \rangle \cup \left \langle {\pi \over 3} + k\pi; {\pi \over 2} + k\pi\right)\Big\}\ .
- Príklad 3
- Riešte goniometrickú nerovnicu s neznámou x \in \mathbb{R}:
\sin x > \cos x Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/zloznerovnice.priklady.inc on line 46
Riešenie
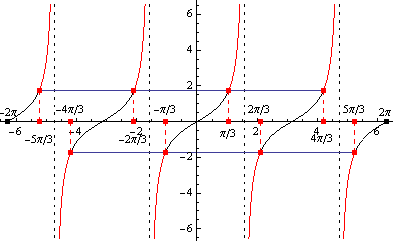
Využijeme graf funkcie sínus a kosínus:

Časť grafu vyznačená červenou farbou zahŕňa riešenie danej nerovnice. Je vidieť, že riešenim pri využití periódy 2\pi je množina K = \bigcup\limits_{k\in\mathbb{Z}} \left ({\pi \over 4} + 2k\pi; {5 \over 4}\pi + 2k\pi \right ).
- Príklad 4
- Riešte goniometrickú nerovnicu s neznámou x \in \langle 0; 2\pi \rangle:
\cos 2x + \sin x < 1
Riešenie
\cos^2 x - \sin^2 x + \sin x < 1 (Použili sme vzorec \cos 2x = \cos^2 x - \sin^2 x.)
(1- \sin^2 x) - \sin^2 x + \sin x < 1 (Použili sme vzorec \cos^2 x + \sin^2 x = 1.)
1 - 2\sin^2 x + \sin x < 1
- 2\sin^2 x + \sin x < 0
\sin x(-2\sin x + 1) < 0 (Využijeme vlastnosť, kedy je súčin dvoch čísel menší ako nula.)
\sin x(-2\sin x + 1) < 0 \Leftrightarrow (\sin x < 0 \wedge -2\sin x + 1 > 0) \vee (\sin x > 0 \wedge -2\sin x + 1 < 0)
Riešenie sa nám rozdelí na dva prípady.
Prvá možnosť:
\sin x < 0 \wedge -2\sin x + 1 > 0
\sin x < 0 Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/zloznerovnice.priklady.inc on line 68
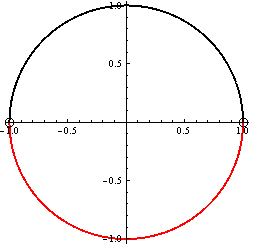
Z jednotkovej kružnice plynie, že \sin x < 0 \Rightarrow K_{11}= (\pi; 2\pi).
-2\sin x + 1 > 0
\sin x < {1 \over 2} Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/zloznerovnice.priklady.inc on line 72
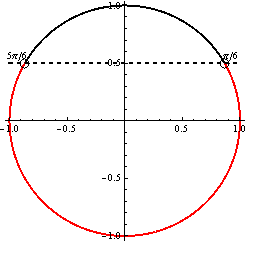
Z jednotkovej kružnice plynie, že \sin x < {1 \over 2} \Rightarrow K_{12}= \left(0; {\pi \over 6}\right) \cup \left({5 \over 6}\pi; 2\pi\right).
K_1 = K_{11} \cap K_{12}
K_1 = (\pi; 2\pi)
Druhá možnosť:
\sin x > 0 \wedge -2\sin x + 1 < 0
\sin x > 0 Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/zloznerovnice.priklady.inc on line 80
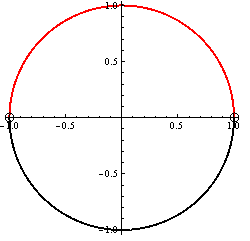
Z jednotkovej kružnice plynie, že \sin x > 0 \Rightarrow K_{21}= (0; \pi).
-2\sin x + 1 < 0
\sin x > {1 \over 2} Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/zloznerovnice.priklady.inc on line 84
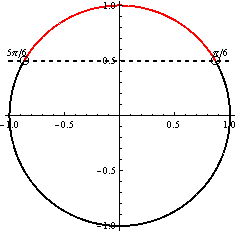
Z jednotkovej kružnice plynie, že \sin x > {1 \over 2} \Rightarrow K_{22}= \left({\pi \over 6}; {5 \over 6}\right).
K_2 = K_{21} \cap K_{22}
K_2 = \left({\pi \over 6}; {5 \over 6}\right)
K = K_{1} \cup K_{2} (Celkově riešenie je zjednotením dvoch čiastkových.)
Výsledné riešenie zapíšeme v tvare K = \left ({\pi \over 6}; {5 \over 6}\pi \right ) \cup \left(\pi; 2\pi \right).
- Príklad 5
- Riešte goniometrickú nerovnicu s neznámou x \in \mathbb{R}:
-2\sin^2 x + 5\cos x +4 \geq 0
Riešenie
-2(1 - \cos^2 x) + 5\cos x +4 \geq 0 (Použili sme vzorec \cos^2 x + \sin^2 x = 1.)
2\cos^2 x + 5\cos x + 2 \geq 0
Zavedieme substitúciu \cos x = a
2a^2 + 5a + 2 \geq 0 (Určíme diskriminant a korene odpovedajúcej kvadratickej rovnice.)
D = 5^2 - 4\cdot 2 \cdot 2 = 9
Riešenia kvadratickej rovnice teda sú:
a_{1,2}= \large {-5 \large \pm 3 \large \over \large 2\cdot 2}, čiže a_1={-1\over 2}; a_2 = -2
Nájdené korene využíjeme k tomu, aby sme kvadratický trojčlen v nerovnici rozložili na súčin.
2\left(a + {1 \over 2}\right)\cdot (a+2) \geq 0 (Vrátime sa k substitúcií \cos x = a.)
(2\cos x + 1)(\cos x + 2) \geq 0 (Využijeme vlastnosť, kedy je súčin dvoch čísel väčší ako nula.)
(2\cos x + 1)(\cos x + 2) \geq 0 \Leftrightarrow (2\cos x + 1 \geq 0 \wedge \cos x + 2 \geq 0) \vee (2\cos x + 1 \leq 0 \wedge \cos x + 2 \leq 0)
Riešenie sa nám rozdelí na dva prípady.
Prvá možnosť:
2\cos x + 1 \geq 0 \wedge \cos x + 2 \geq 0
\cos x \geq -{1 \over 2} \wedge \cos x \geq -2, odkiaľ plynie, že \cos x \geq -{1 \over 2} Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/zloznerovnice.priklady.inc on line 118
Situáciu si znázornime na jednotkovej kružnici.
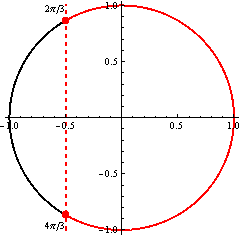
Využitím jednotkovej kružnice, periodičnosti funkcie kosínus, platí -{2 \over 3}\pi + 2\pi = {4 \over 3}\pi, dostávame riešenie, ktoré zapíšeme v tvare K = \bigcup\limits_{k\in\mathbb{Z}} \left \langle -{2 \over 3}\pi + 2k\pi; {2 \over 3}\pi + 2k\pi \right \rangle.
Druhá možnosť:
2\cos x + 1 \leq 0 \wedge \cos x + 2 \leq 0
\cos x \leq -{1 \over 2} \wedge \cos x \leq -2, odkiaľ plynie, že \cos x \leq -2
\cos x \leq -2 \Rightarrow x \in \emptyset (Plynie z oboru funkčných hodnôt funkcie kosínus.)
Odkiaľ plynie, že množina koreňov je prázdna, čo matematický zapíšeme ako K_2 = \emptyset
K = K_{1} \cup K_{2} (Celkově riešenie je zjednotením dvoch čiastkových.)
Výsledné riešenie zapíšeme v tvare K = \bigcup\limits_{k\in\mathbb{Z}}\left \langle -{2 \over 3}\pi + 2k\pi; {2 \over 3}\pi + 2k\pi \right \rangle.