Pozn. Pojmem proměnná označujeme libovolné písmeno, které zastupuje čísla z určitého oboru. Tento obor nazýváme obor proměnné. Konkrétní čísla, která se objevují ve výrazech, označujeme jako konstanty.

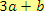
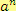
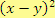
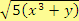
Výraz je např. zápis , , , . Výrazem naopak není zápis .

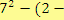
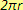
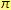
Pro lepší pochopení uvedených pojmů se podíváme na výraz , pomocí něhož vypočítáme obvod kruhu. Jedná se o výraz, kde konstantami jsou čísla 2 a (jejich hodnota je stále stejná, konstantní). Proměnnou je v tomto případě písmeno , vyjadřující poloměr daného kruhu (hodnota poloměru se pro různé kruhy mění, proměňuje se, a s ní i obvod kruhu).

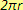
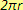
A jaký je obor proměnné pro výraz ? Díváme-li se na tento výraz jako na návod pro výpočet obvodu kruhu, tak obor proměnné je tvořen všemi kladnými čísly (poloměr kruhu, tedy proměnná , nemůže nabývat záporných hodnot ani nuly). Jestliže však výraz chápeme obecněji, jako určitý výraz se dvěma konstantami a jednou proměnnou, pak do oboru proměnné zahrnujeme všechna reálná čísla.

Kromě oboru proměnné existuje i definiční obor proměnné. Do definičního oboru proměnné patří jen taková čísla, pro které daný výraz má smysl. To znamená, že po dosazení libovolného čísla z definičního oboru proměnné nenastane nepřípustná operace (dělení nulou, výraz nula na nultou, odmocňování záporného čísla, atd.). V našem případě je definiční obor proměnné tvořen všemi reálnými čísly.

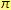
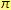
Pozn. Pozorný čtenář jistě zpozoroval, že řecké písmeno [pí] jsme označili jako konstantu. Jak již víme z kapitoly o číselných oborech, písmeno reprezentuje iracionální Ludolfovo číslo (jeho přibližná hodnota je 3,14).

Pozn. Není-li v zadání úlohy obor proměnné uveden, bereme v úvahu ten nejobecnější možný (obvykle obor reálných čísel). Z tohoto oboru vynecháme ty hodnoty, pro které výraz nemá smysl, a tím dostaneme definiční obor proměnné.

Pozn. Do definičního oboru výrazu s více proměnnými patří jen taková čísla, pro která má daný výraz smysl.


Příklad[nahoru]
Urči, pro které hodnoty jednotlivých reálných proměnných má daný výraz smysl:
a)
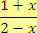Řešení
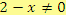
Výraz má smysl pro všechna taková, že , tj. .
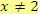
Pro by nastala nepřípustná operace dělení nulou.
Tedy .

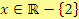
b)
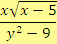Řešení
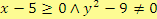
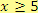
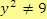
Aby měl výraz smysl, musí zároveň platit: . První podmínku lze přepsat jako , druhou jako , tj. .
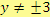
První podmínka zaručuje, že nebudeme odmocňovat záporné číslo. Druhá podmínka vylučuje dělení nulou.
Tedy .

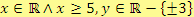
c)
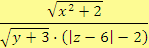Řešení
Aby daný výraz měl smysl, musí zároveň platit:
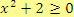
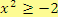
1. , tj. . Tato podmínka platí pro všechna , protože druhá mocnina libovolného čísla je vždy větší nebo rovna nule.
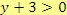
2. , tj. .
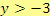
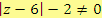
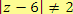
3. , tj. , tedy .
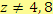
První podmínka nám zaručí, že nebudeme odmocňovat záporné číslo. Druhou podmínkou vyloučíme pod odmocninou všechna záporná čísla i nulu, abychom neodmocňovali záporné číslo ani nedělili nulou. Třetí podmínka zaručuje, že nebudeme dělit nulou.
Tedy , , .

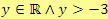
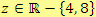
Příklad[nahoru]
Urči hodnotu výrazu pro dané hodnoty proměnných:
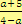
a) , pro
Řešení


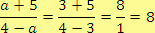
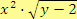
b) , pro
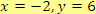Řešení


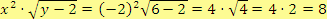
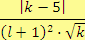
c) , pro
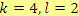Řešení


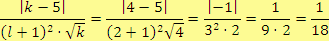
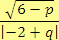
d) , pro
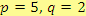Řešení
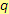
Pro zvolené hodnoty proměnných výraz nemá smysl. Po dosazení za proměnnou ve jmenovateli by nastala nepřípustná operace, a to dělení nulou.


S výrazy se v matematickém textu setkáváme často. Přehledný a snáze srozumitelný výraz totiž nahrazuje zdlouhavý slovní popis. Srovnej: Podíl pětinásobku součtu dvou reálných čísel a druhé odmocniny z jejich rozdílu jednoduše zapíšeme jako .

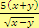
Příklad[nahoru]
Zapiš jako výraz se zvolenými proměnnými (např. , ):
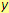
a) součet šestinásobku třetí mocniny prvního čísla a třetiny absolutní hodnoty druhého čísla
Řešení

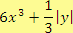
b) rozdíl druhé odmocniny dvojnásobku prvního čísla a druhé mocniny čtyřnásobku druhého čísla
Řešení

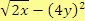
c) součin dvojnásobku prvního čísla a čtvrtiny druhé odmocniny druhého čísla
Řešení

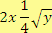
d) podíl čtvrté mocniny prvního čísla a absolutní hodnoty dvojnásobku druhého čísla
Řešení



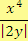
S výrazy se setkáváme také v podobě vzorců, a to nejen v matematice, ale i v dalších vědách – fyzice, chemii, zeměpisu (např. vzorec pro objem kvádru, výpočet rychlosti podle dráhy a času, vzdálenost dvou míst na Zemi podle jejich souřadnic). Výrazy nám pomáhají i při zápisu řešení slovních úloh.

Příklad[nahoru]
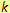
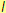
Petra má 3 sáčky, v každém z nich je bonbónů. Tyto bonbóny chce rozdělit mezi svých spolužáků. Pomocí výrazu napiš, o kolik se zmenší počet bonbónů pro každého spolužáka, jestliže Petra chce obdarovat i kamarádů z vedlejší třídy, a během cesty do školy už 5 % bonbónů snědla.

Řešení
Původní počet bonbonů pro každého spolužáka…
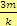
Počet spolužáků a kamarádů z vedlejší třídy…
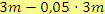
Počet bonbonů, které má Petra po příchodu do školy…, tj.
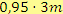
Počet bonbonů, které dostane každý spolužák nebo kamarád…
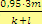
Zmenšení počtu bonbonů připadajících na spolužáka…


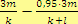
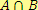
Pozn. V této kapitole pracujeme s algebraickými výrazy, tj. s výrazy, v nichž za každou proměnnou dosazujeme z číselného oboru. Existují ale i nealgebraické výrazy, jako např. výraz . S nealgebraickými výrazy se setkáváme např. ve výrokové logice. Většinou lze z kontextu poznat, kdy výraz je či není algebraický. Proto můžeme slovo algebraický vynechat.

Cvičení k této kapitole.[nahoru]