Čísla

se nazývají
koeficienty mnohočlenu, sčítanci
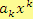
se nazývají
členy mnohočlenu. Pro některé členy mnohočlenu máme speciální pojmenování. Člen
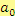
se nazývá
absolutní člen mnohočlenu. Člen
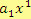
se nazývá
lineární člen a člen
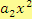
se nazývá
kvadratický člen mnohočlenu.
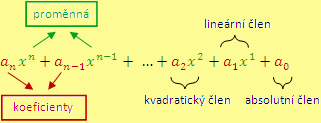 Stupeň mnohočlenu
Stupeň mnohočlenu odpovídá nejvyššímu exponentu proměnné v mnohočlenu.
- Mnohočlen 1. stupně (tj. výraz
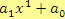 , také lze zapsat jako
, také lze zapsat jako  )
se nazývá lineární.
)
se nazývá lineární.
- Mnohočlen 2. stupně (tj. výraz
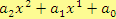 , také lze zapsat jako
, také lze zapsat jako 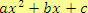 )
se nazývá kvadratický.
)
se nazývá kvadratický.
- Mnohočlen nultého stupně je každé reálné číslo různé od nuly.
- Číslo nula nazýváme nulový mnohočlen, jeho stupeň nedefinujeme.
Mnohočlen s jedním členem označujeme jako
jednočlen, se dvěma členy jako
dvojčlen,
se třemi členy jako
trojčlen, atd.
Například
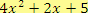
je kvadratický mnohočlen, tj. mnohočlen 2. stupně, s proměnnou

.
Jedná se o trojčlen (má tři sčítance). Koeficient u kvadratického členu je 4, koeficient u lineárního členu je 2. Absolutní člen je roven 5.
Mnohočleny mohou mít obecně i více proměnných. Jako příklad mnohočlenu se dvěma proměnnými lze uvést výrazy

,
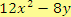
. Příkladem mnohočlenu se třemi proměnnými jsou výrazy
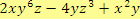
,
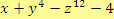
.
Z předcházejících kapitol již víme, že sčítat a odčítat můžeme jen ty mocniny, které mají stejný základ a stejného mocnitele. U mnohočlenů bude platit obdobné pravidlo.
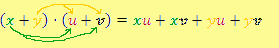 Příklad[nahoru]
Příklad[nahoru]
Vypočítej:
a)
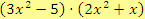 Řešení
Řešení
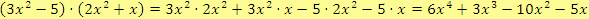
b)
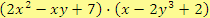 Řešení
Řešení
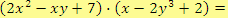
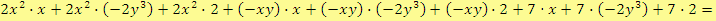
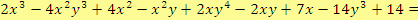
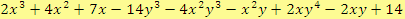
Počítáme-li součet, rozdíl nebo součin tří a více mnohočlenů, postupujeme obdobně.
Pokud umíme mnohočleny násobit, můžeme vypočítat i jejich
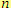
-tou mocninu pro všechna
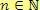
. Druhou a třetí mocninu dvojčlenu můžeme také určit podle následujících vzorců:
Pozn. Je výhodné si tyto vzorce zapamatovat, neboť jejich použití usnadní mnohé výpočty, což dokládá následující příklad.
Příklad[nahoru]
Vypočítej:
a)
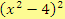 Řešení
Řešení
 Jiný způsob řešení
Jiný způsob řešení
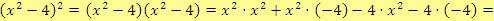
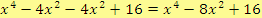
Součtem, rozdílem a součinem libovolných mnohočlenů je vždy mnohočlen.
Příklad[nahoru]
Vypočítej za předpokladu, že
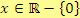
:
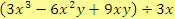 Řešení
Řešení
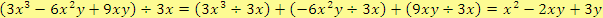
Podílem mnohočlenů nemusí být vždy mnohočlen.
Jestliže podílem mnohočlenů je mnohočlen, mluvíme o dělení mnohočlenů beze zbytku (viz předchozí příklad). Jestliže podílem mnohočlenů není mnohočlen, mluvíme o dělení mnohočlenů se zbytkem (viz následující příklad). Vzniklý výraz si můžeme rozdělit na dvě části.
První část tvoří výraz, který je mnohočlenem, tzv.
neúplný podíl. Druhou částí je výraz, který není mnohočlenem, označujeme jej jako
zbytek.
Pozn. Terminologie je obdobná jako u dělení čísel.
Příkladem dělení čísel beze zbytku je např. výraz
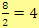
. Jako příklad dělení čísel se zbytkem lze uvést výraz
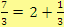
.
Příklad[nahoru]
Vypočítej za předpokladu, že
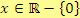
:
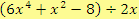 Řešení
Řešení
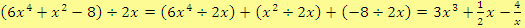
Mnohočlen
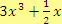
je neúplný podíl. Člen
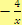
je zbytek (mocnina u proměnné v mnohočlenu může nabývat pouze libovolných kladných hodnot nebo nuly. V tomto členu je však rovna -1, jelikož
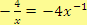
,
proto tento výraz není mnohočlenem).
A jak vypočítáme
podíl mnohočlenů? Omezíme se jen na případy mnohočlenů s jednou proměnnou, kdy bude zároveň platit, že stupeň mnohočlenu, který dělíme, je vyšší nebo roven stupni mnohočlenu, který je dělitelem. Postup je pak následující:
1. Nejdříve si členy obou mnohočlenů uspořádáme sestupně (tj. na prvním místě bude člen s proměnnou s nejvyšším exponentem).
2. První člen dělence vydělíme prvním členem dělitele, výsledek je prvním členem podílu mnohočlenů.
3. Pak tímto dílčím výsledkem vynásobíme všechny členy dělitele a tento výraz odečteme od dělence.
4. Tím dostaneme nový mnohočlen. Pokud je tento nový mnohočlen vyššího nebo stejného stupně jako dělitel, zopakujeme celý postup.
5. Takto pokračujeme dál, dokud nedostaneme mnohočlen nižšího stupně než je dělitel nebo nulu.
Pozn. Ve výrazu
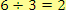
je dělencem číslo 6, dělitelem číslo 3 a číslo 2 je jejich podíl.
Příklad[nahoru]
Vypočítej a stanov podmínky:
a)
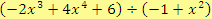 Řešení
Řešení
1.
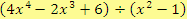
2.
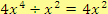
3.
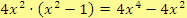

Tyto kroky se většinou zapisují následovně:
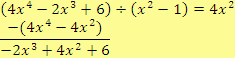
4.
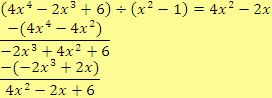
5.
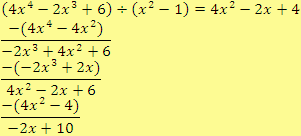
V tomto případě je mnohočlen
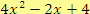
neúplný podíl, výraz
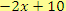
je zbytek. Pro všechna
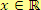
, pro které je
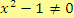
, tj.
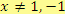
, platí:
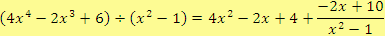
O správnosti výsledku se můžeme přesvědčit zkouškou:
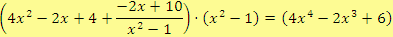
b)
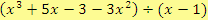 Řešení
Řešení
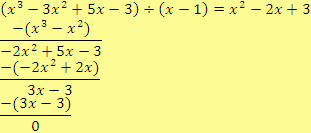
V tomto případě se jedná o dělení beze zbytku.
Pro všechna
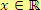
, pro které je
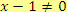
,
tj.
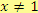
, platí:
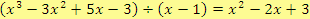
O správnosti výsledku se můžeme přesvědčit zkouškou:
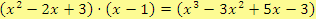 Cvičení
Cvičení k této kapitole.
[nahoru]