ČÍSELNÉ OBORY
Číselným oborem rozumíme číselnou množinu, na které jsou definovány bez omezení početní operace sčítání a násobení,
tj. číselný obor je vzhledem k těmto operacím uzavřený.
Pozn. Uzavřenost číselného oboru vzhledem k početní operaci znamená, že výsledkem početní operace mezi dvěma libovolnými prvky z příslušné číselné množiny je číslo,
které také patří do této číselné množiny.
Obor všech přirozených čísel je tvořen množinou čísel
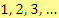
, na které jsou definovány bez omezení početní operace sčítání a násobení.
Značíme
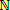
.
Obor všech celých čísel je tvořen množinou obsahující všechna přirozená čísla, všechna čísla opačná k přirozeným číslům a nulu, na které jsou definovány bez omezení početní operace sčítání, odčítání a násobení.
Značíme
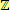
.
Pozn.
Opačným číslem 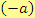
k číslu

rozumíme takové číslo, pro něhož je
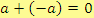
.
Opačné číslo ke kladnému číslu je číslo záporné (např.

,
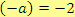
), opačné číslo k zápornému číslu je číslo kladné
(např.

,
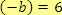
).
Opačné číslo k číslu nula je číslo nula.
Příklad[nahoru]
Rozhodni, zda-li následující tvrzení jsou pravdivá:
a) Číslo
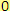
náleží do oboru přirozených čísel.
Řešení
Ne, číslo
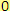
náleží do oboru celých čísel.
b) Opačným číslem k číslu
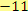
je číslo
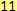
.
Řešení
Ano, toto tvrzení je pravdivé.
c) Číslo
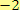
náleží do oboru přirozených čísel.
Řešení
Ne, číslo
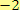
náleží do oboru celých čísel.
Obor všech racionálních čísel je tvořen množinou obsahující taková čísla, která lze zapsat ve tvaru

, kde
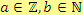
,
na které jsou definovány bez omezení početní operace sčítání, odčítání, násobení a dělení nenulovým číslem.
Značíme
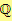
.
Pozn. Množinu racionálních čísel můžeme také popsat tak, že obsahuje čísla s konečným desetinným rozvojem (např. číslo
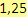
)
a nekonečným periodickým desetinným rozvojem (např. číslo

).
Obor všech reálných čísel je tvořen množinou obsahující všechna racionální čísla a čísla s nekonečným neperiodickým desetinným rozvojem, na které jsou definovány bez omezení početní operace sčítání, odčítání, násobení a dělení nenulovým číslem.
Značíme
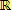
.
Pozn. Reálné číslo, které zároveň nepatří do množiny racionálních čísel, nazýváme
iracionální číslo. Příkladem iracionálního čísla je číslo
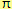
,
(tj. Ludolfovo číslo, které představuje podíl obvodu libovolné kružnice a jejího průměru), které má nekonečný neperiodický desetinný rozvoj.
Pozn. Každé reálné číslo můžeme znázornit jako bod na číselné ose. A zároveň každý bod na číselné ose reprezentuje jedno reálné číslo.
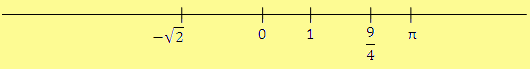
Pozn. Zápis
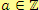
čteme

náleží
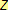
.
Tento zápis znamená, že číslo

je prvkem oboru celých čísel.
Příklad[nahoru]
Rozhodni, zda platí:
a)
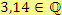 Řešení
Řešení
Ano, protože se jedná o číslo s konečným desetinným rozvojem.
b)
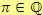 Řešení
Řešení
Ne, Ludolfovo číslo má nekonečný neperiodický desetinný rozvoj, proto do oboru racionálních čísel nepatří.
c)
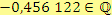 Řešení
Řešení
Ano, protože se jedná o číslo s konečným desetinným rozvojem.
Vztah mezi číselnými množinami lze schematicky vyjádřit:
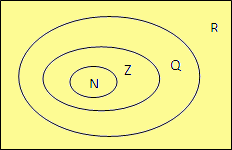
Na závěr se podíváme, jaké vlastnosti má každý číselný obor:
Pro každá tři čísla

,
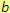
,

z číselného oboru platí:
1. asociativnost sčítání a násobení
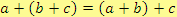
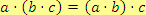
2. komutativnost sčítání a násobení
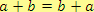

3. existence neutrálního prvku vzhledem ke sčítání a násobení
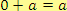
(s výjimkou oboru přirozených čísel)
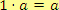
4. distributivnost násobení vzhledem ke sčítání
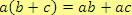
Pozn.
Neutrální prvek vzhledem k početní operaci je takový prvek, který neovlivní výsledek početní operace.
Pozn. V oboru přirozených čísel platí existence neutrálního prvku jen vzhledem k násobení. Existence neutrálního prvku vzhledem ke sčítání v něm neplatí, protože do oboru přirozených čísel nezahrnujeme číslo 0.
[nahoru]