V matematice se setkáváme se složitými výpočty, přesto se matematikové snaží zapisovat své výsledky
a výpočty co nejelegantněji, aby byly stručné a přehledné. Proto se místo zápisu
používá elegantnější zápis
. Obdobně místo součinu
píšeme
, tedy zápis pomocí mocniny.
a každé přirozené číslo
platí:
nazýváme mocnina,
je základ mocniny (mocněnec),
je mocnitel (exponent).
platí 
,
platí 
a 
.
, tak je mocnina vždy kladná, což vidíme přímo z definice (součin kladných čísel je kladné číslo).
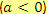, tak mohou nastat dva případy. Když je mocnitel sudé číslo, pak je mocnina číslo kladné (součin sudého počtu záporných čísel je číslo kladné). Je-li však mocnitel liché číslo, pak mocnina je číslo záporné (součin lichého počtu záporných čísel je číslo záporné).
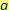
číslo kladné:a)  | Ano, protože  . |
b)  | Ne, protože  a je liché. |
c)  | Ano, protože . |
d)  | Ano, protože a je sudé. |
e)  | Ne, protože a je liché. |
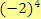
a 
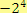
. V prvním případě je 
,
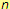
tj. a zároveň je sudé,
proto je podle tabulky tato mocnina číslo kladné. Tento výraz můžeme také přepsat jako 
.
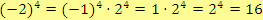
Ve druhém případě se vlastně jedná o výraz 
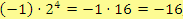
, tudíž výsledek je číslo záporné.
, 
a pro každá
přirozená čísla 
, 
platí:
,
,
,
,
.
