Lineární rovnice
Stručně zopakujeme početní řešení lineárních rovnic, pro podrobnější informace navštivte stránku Jaromíra Gloce. Zaměříme se spíše na grafické řešení lineárních rovnic.
Definice
Nechť a, b jsou reálná čísla a a \neq 0. Potom rovnici ve tvaru ax + b = 0 nazýváme lineární rovnicí s neznámou x \in \mathbb{M}.
Početní řešení
Při řešení lineárních rovnic používáme ekvivalentní úpravy.
Množina všech řešení lineární rovnice ax + b = 0 v \mathbb{R} , kde a \neq 0, je \mathbb{K} = \left \{ -\frac{b}{a} \right \} .
Pokud budeme řešit rovnici např. v množině celých čísel a číslo -\frac{b}{a} není celé číslo, množina všech řešení je \mathbb{K} = \emptyset . Proto je důležité dávat pozor na to, v jaké množině čísel \mathbb{M} danou rovnici řešíme.
Pokud bychom uvažovali a = 0, tak v případě, že b \neq 0 nemá rovnice smysl a \mathbb{K} = \emptyset . V případě, že i b = 0 je řešením rovnice \mathbb{K} = \mathbb{M} .
ÚlohaŘešte rovnici \frac{x - 2}{3} = \frac{3x + 1}{2} s neznámou x \in \mathbb{R} .
Speciální způsob řešení mají rovnice v součinovém tvaru. Jde o tvar rovnice, kde se součin dvou nebo více lineárních dvojčlenů rovná nule:
Postup řešení takové rovnice je založen na tvrzení:
Součin dvou a více výrazů je roven nule právě tehdy, když je alespoň jeden z výrazů roven nule.
Řešte rovnici (x - 5)*(x + 1) = (x - 5) s neznámou x \in \mathbb{R} .
Grafické řešení
Lineární rovnice s neznámou x \in \mathbb{R} lze řešit i graficky. Grafem funkce f : y = ax + b je přímka. Funkce f se nazývá lineární funkce. V následujícím appletu můžete pomocí změny posuvníků pozorovat, jak vypadá graf funkce f : y = ax + b při změně parametrů a, b \in \mathbb{R}.
Postup při grafickém řešení lineární rovnice ve tvaru ax + b = cx + d, kde a, b, c, d \in \mathbb{R} a x \in \mathbb{R} je neznámá:
- Levou stranu rovnice chápeme jako předpis funkce f : y = ax + b a pravou stranu jako předpis funkce g : y = cx + d.
- Grafem funkcí f, g jsou přímky. Hledané kořeny lineární rovnice získáme sestrojením obou grafů funkcí f a g.
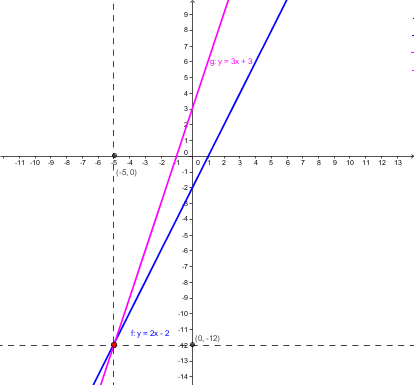
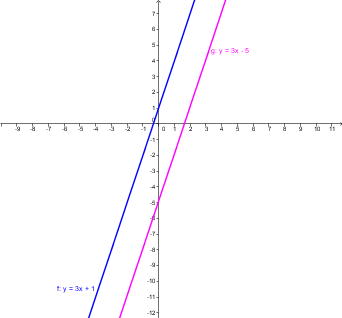
- Řešením lineární rovnice jsou x-ové souřadnice průsečíků grafů funkcí f, g. Pro názornost se podívejme na následující applet, kde se opět dají měnit koeficienty v předpisu funkcí pomocí změny posuvníků.
Množinou všech řešení lineární rovnice je:
- x-ová souřadnice průsečíku P=[x_P, y_P], \mathbb{K} = \left \{ x_P \right \}, a to pokud jsou přímky různoběžné.
- prázdná množina \mathbb{K} = \emptyset, pokud jsou přímky rovnoběžné různé.
- množina \mathbb{K} = \mathbb{M}, pokud přímky splývají.
Poznámka
Grafické řešení lineární rovnice ve tvaru ax + b = 0, kde a, b \in \mathbb{R} a x \in \mathbb{R} je neznámá, je shodné s předešlým postupem. Uvědomíme-li si, že nulu na pravé straně rovnice lze chápat jako předpis funkce g: y = 0, jejíž graf je přímka splývající s osou x.
V appletu výše nastavte parametry c, d na nulu a pozorujte polohu přímky ax + b = y vzhledem k ose x.