Důležité pojmy - opakování
Než si ukážeme, jak řešit binomické rovnice, zopakujeme některé pojmy z učiva o komplexních číslech. Podrobné informace o komlexních číslech a následujících pojmech můžete najít na stránkách Lenky Šilarové.
Goniometrický tvar komplexního čísla
V Gaussově rovině je dán bod Z=[x, y], který je obrazem nenulového komplexního čísla z = x + iy, kde i je imaginární jednotka a x, y \in \mathbb{R}.
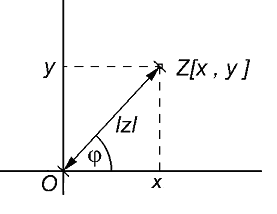
Číslo x je reálná čast komplexního čísla z a platí x = |z|cos \varphi.
Číslo y je imaginární čast komplexního čísla z a platí y = |z|sin \varphi.
Po dosazení x a y do z získáme goniometrický tvar komplexního čísla z=|z|(cos \varphi + i sin \varphi).
Číslo \varphi nazýváme argument komplexního čísla, \varphi \in \left \langle 0, 2\pi \right \rangle.
Číslo |z| nazýváme absolutní hodnota komplexního čísla a platí |z| = \sqrt{{x}^2+{y}^2} .
cos \varphi = \frac{x}{|z|}, sin \varphi = \frac{y}{|z|}
N-tá mocnina komplexního čísla
Je dáno nenulové komplexní číslo z v goniometrickém tvaru z=|z|(cos \varphi + i sin \varphi) a přirozené číslo n. Pak n-tá mocnina čísla z je tvaru z^n ={|z|}^n (cos n \varphi + i sin n \varphi).
N-tá odmocnina komplexního čísla
Je dáno nenulové komplexní číslo a a přirozené číslo n. Pak číslo z=|z|(cos \varphi + i sin \varphi) je řešením rovnice z^n = a, kde a=|a|(cos \alpha + i sin \alpha). Všechna řešení rovnice lze psát ve tvaru
z_k =\sqrt[n]{|a|} \Big[ cos ( \frac {\alpha + 2k \pi}{n} ) + i sin ( \frac {\alpha + 2k \pi}{n}) \Big] , kde k = 0, 1, ..., (n-1) .
Čísla z_k jsou hodnoty komplexní n-té odmocniny čísla a. Značíme: {(\sqrt[n]{a})}_c
Poznámka
Je důležité rozlišovat n-tou odmocninu z reálného čísla a n-tou odmocninu z komplexního čísla. Odmocnina z reálného čísla je jednoznačná, narozdíl od odmocniny z komplexního čísla.