Grafické řešení kubických rovnic
Každou algebraickou rovnici s neznámou x \in \mathbb{R} lze řešit nejen početně, ale i graficky. Tedy i kubické rovnice lze řešit graficky.
Při grafickém řešení kubických rovnic budeme postupovat podobně, jako při řešení rovnic kvadratických. Kubickou rovnici lze také řešit graficky dvěma způsoby.
Uvažujme kubickou rovnici tvaru ax^3 + bx^2 + cx + d = 0 , kde a, b, c, d \in \mathbb{R} a x \in \mathbb{R} je neznámá.
1. způsob řešení
První způsob grafického řešení spočívá v hledání průsečíků grafu mocninné funkce s lichým exponentem, zvaném kubická parabola, a paraboly.
Postup při grafickém řešení kubické rovnice:
- Kubickou rovnici ax^3 + bx^2 + cx + d = 0 upravíme na tvar ax^3 = -bx^2 - cx - d .
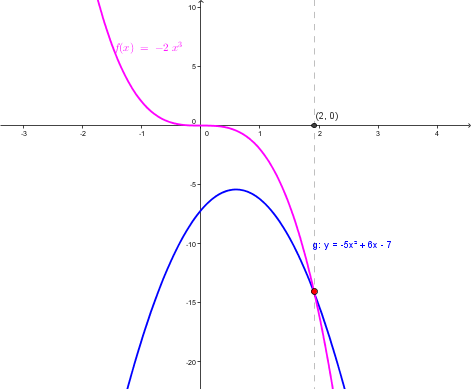
- Levou stranu rovnice chápeme jako předpis mocninné funkce s lichým exponentem f : y = ax^3 a pravou stranu jako předpis funkce g: y = -bx^2 - cx - d , což je také mocninná funkce (resp. kvadratická), ale se sudým exponentem, jejímž grafem je parabola.
- Sestojíme grafy funkcí f, g. Graf mocninné funkce f: y=ax^3 nazýváme kubickou parabolou. Kubická parabola prochází počátkem a body [1,1], [-1,-1]. Grafem funkce g je parabola, jak jsme si řekli již u kvadratických rovnic.
- Řešením kubické rovnice jsou x-ové souřadnice průsečíků grafů funkcí f, g. Pro názornost se podívejme na následující applet, kde se dají měnit koeficienty v předpisu funkcí pomocí změny posuvníků.
Ve speciálním případě, kdy je koeficient b u kvadratického členu nulový, je grafem funkce g přímka. Hledáme tedy x-ové souřadnice průsečíků mocninné funkce f: y=ax^3 a lineární funkce g: y= -cx - d.
Úloha
Řešte rovnici -2x^3 + 5x^2 - 6x + 7 = 0 s neznámou x \in \mathbb{R} graficky.
2. způsob řešení
Druhý způsob grafického řešení spočívá v hledání průsečíků grafu mocninné funkce s lichým exponentem, zvaném kubická parabola, a osy x.
Postup při grafickém řešení kubické rovnice:
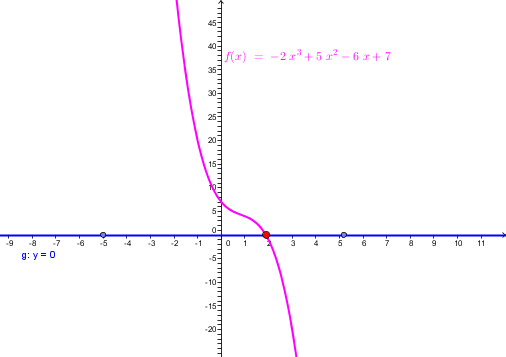
- Levou stranu rovnice chápeme jako předpis mocninné funkce s lichým exponentem f : y = ax^3 + bx^2 + cx + d a pravou stranu jako předpis funkce g : y = 0.
- Sestojíme grafy funkcí f, g. Graf funkce f nazýváme kubickou parabolou. Grafem funkce g je přímka, která splývá s osou x.
- Řešením kubické rovnice jsou x-ové souřadnice průsečíků grafu funkce f a osy x. Pro názornost se podívejme na následující applet, kde se opět dají měnit koeficienty v předpisu funkce pomocí změny posuvníků.
Úloha
Řešte rovnici -2x^3 + 5x^2 - 6x + 7 = 0 s neznámou x \in \mathbb{R} graficky.