Titulní stránka
Úvodní stránka
Pythagorova věta
Goniometrické funkce ostrého úhlu
Sinová věta
Kosinová věta
Tangentová věta
Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Tangentová věta
V každém trojúhelníku 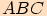 , jehož vnitřní úhly mají velikosti
, jehož vnitřní úhly mají velikosti
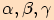 a strany délky
a strany délky 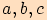 ,
platí
,
platí
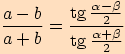 .
.
Tangentová věta
Poznámka. Další vyjádření tangentové věty dostaneme cyklickou záměnou.
Jsou to vzorce:
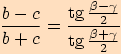
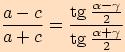
Důkaz

K důkazu použijeme sinovou větu a vzorce pro goniometrické funkce .
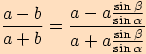
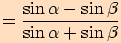
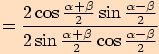
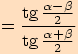
Věta o polovičních úhlech
V každém trojúhelníku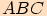 , jehož vnitřní úhly mají velikosti
, jehož vnitřní úhly mají velikosti
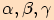 a strany délky
a strany délky  ,
platí
,
platí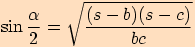
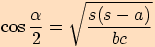
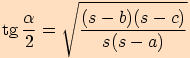 , kde
, kde 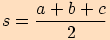 .
.
Důkaz
 Nejprve vyjádříme
Nejprve vyjádříme 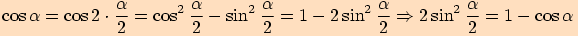 (viz Vzorce pro goniometrické funkce)
(viz Vzorce pro goniometrické funkce)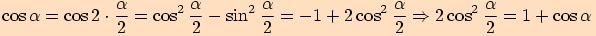
Dále z kosinové věty vyjádříme
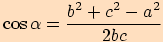
a dosadíme do předchozích vyjádření
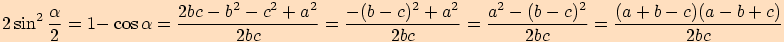
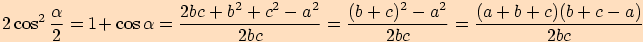 .
.Jestliže označíme
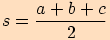 ,
potom pro trojčleny v čitatelích zlomků plyne
,
potom pro trojčleny v čitatelích zlomků plyne 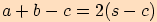
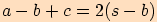
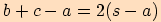
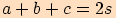
Po dosazení těchto čitatelů dostáváme
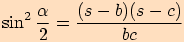 ,
,
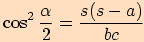 .
.Nyní oba vztahy odmocníme (to můžeme udělat, neboť neexistuje trojúhelník s nulovým nebo záporným úhlem a tudíž
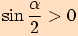 ,
,
 , také
, také
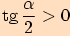 ) a dostaneme vztahy, které jsme chtěli dokázat.
) a dostaneme vztahy, které jsme chtěli dokázat. >>nahoru<<
Příklady
1.
 velikosti ostatních úhlů, jestliže
velikosti ostatních úhlů, jestliže 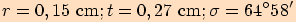 .
. 
Dosadíme do tangentové věty
velikosti příslušných úhlů a upravujeme.
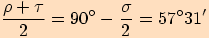

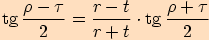

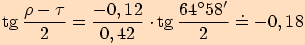

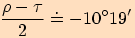

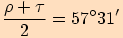

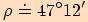



2.
V trojúhelníku  , kde
, kde 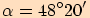 ,
,
 ,
,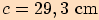 , vypočítejte
pomocí tangentové věty délku strany
, vypočítejte
pomocí tangentové věty délku strany 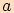 .
.

Dosadíme do tangentové věty
velikosti příslušných úhlů a upravujeme.
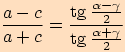

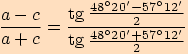

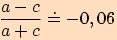

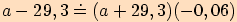

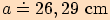

3. Vypočítejte velikosti vnitřních úhlů v trojúhelníku
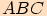 ,
se stranami
,
se stranami 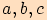 , které mají po řadě délky
, které mají po řadě délky
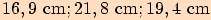 . Použijte větu o polovičních úhlech.
. Použijte větu o polovičních úhlech. 
Nejprve vypočteme poloviční obvod.
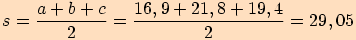

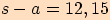

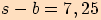

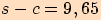

Pro ukázku používám všechny funkce (stačí použít
jednu).
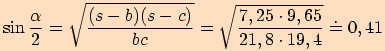

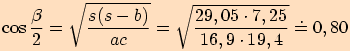

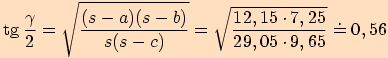

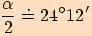

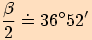

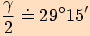

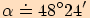

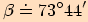



>>nahoru<<