Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Orientovaný úhel
Orientovaným úhlem v rovině rozumíme uspořádanou
dvojici polopřímek se společným počátkem.
Uspořádanou dvojici polopřímek chápeme tak, že jedna z nich je první, nazýváme ji
počátečním ramenem orientovaného úhlu , a druhou nazýváme
koncovým ramenem orientovaného úhlu.
Máme-li konkrétně polopřímky: počáteční 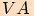 ,
koncová
,
koncová 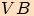 , vzniká nám orientovaný úhel.
Orientovaný úhel označujeme
, vzniká nám orientovaný úhel.
Orientovaný úhel označujeme 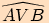 .
Nulové orientované úhly nazýváme úhly, jestliže polopřímky
.
Nulové orientované úhly nazýváme úhly, jestliže polopřímky
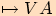 =
= 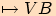 .
.
Jistě nás napadá otázka, zda jsou úhly 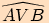 a
a
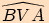 stejné?
stejné?
Nejsou. Vysvětlíme si to pomocí obrázku.
Polopřímky 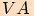 ,
, 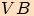 rozdělují rovinu na dva úhly.
Velikosti těchto úhlů označíme
rozdělují rovinu na dva úhly.
Velikosti těchto úhlů označíme 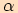 ,
,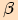 .
Platí
.
Platí 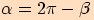 (v míře obloukové),
resp.
(v míře obloukové),
resp. 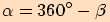 (v míře stupňové).
Tyto úhly si můžeme představit jako množiny všech polopřímek, které vznikly otáčením
polopřímky
(v míře stupňové).
Tyto úhly si můžeme představit jako množiny všech polopřímek, které vznikly otáčením
polopřímky 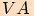 kolem bodu
kolem bodu 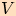 do polohy
polopřímky
do polohy
polopřímky 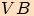 , a to v jednom ze dvou
opačných smyslů. Buď proti směru otáčení hodinových ručiček (zde budeme mluvit
o kladném smyslu otáčení), nebo ve směru pohybu hodinových ručiček (jedná
o záporný smysl otáčení).
, a to v jednom ze dvou
opačných smyslů. Buď proti směru otáčení hodinových ručiček (zde budeme mluvit
o kladném smyslu otáčení), nebo ve směru pohybu hodinových ručiček (jedná
o záporný smysl otáčení).
Orientovaný úhel v záporném smyslu
Orientovaný úhel v kladném smyslu
Velikost toho z úhlů 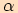 ,
,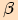 ,
který opíše polopřímka při otočení z počátečního ramene
,
který opíše polopřímka při otočení z počátečního ramene 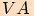 do koncového ramene
do koncového ramene 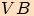 v kladném smyslu se nazývá
v kladném smyslu se nazývá
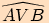 .
Pro základní velikost
.
Pro základní velikost 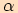 platí, že
platí, že
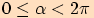 ,
resp.
,
resp.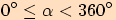 .
.Velikostí orientovaného úhlu
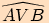 nazýváme každé z reálných čísel
nazýváme každé z reálných čísel 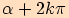 (v míře
obloukové),
resp.
(v míře
obloukové),
resp. 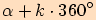 (v míře stupňové), kde
(v míře stupňové), kde 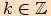 .
.Číslo
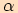 určíme takto
určíme takto-
je-li polopřímka
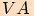 =
=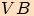 ,
je
,
je 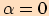 ,
resp.
,
resp.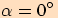
- je-li polopřímka
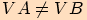 , je
, je 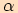 velikost úhlu,
který vznikne otočením počátečního ramene
velikost úhlu,
který vznikne otočením počátečního ramene 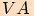 do polohy koncového ramene
do polohy koncového ramene
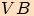 v kladném smyslu otáčení (tj. proti pohybu hodinových ručiček)
v kladném smyslu otáčení (tj. proti pohybu hodinových ručiček)
Poznámka. Při svém otočení totiž polopřímka nemusí
opsat jen úhel 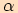 , ale úhel větší. Jedna její "plná otáčka"
v kladném směru je
, ale úhel větší. Jedna její "plná otáčka"
v kladném směru je 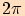 . Takto se může otáčet vícekrát,
přičemž velikosti úhlů jsou
. Takto se může otáčet vícekrát,
přičemž velikosti úhlů jsou 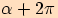 ,
,
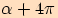 ,
,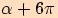 atd.
atd.
Při záporném směru jde o úhel o velikosti 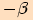 a při několikanásobném otočení
jsou velikosti úhlů tyto
a při několikanásobném otočení
jsou velikosti úhlů tyto 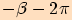 ,
,
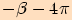 .
Odtud plyne
.
Odtud plyne 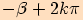 , kde
, kde 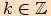 .
.
Součtem orientovaných úhlů 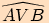 ,
,
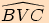 nazýváme úhel
nazýváme úhel 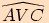 , kde
koncové rameno prvního z nich je počátečním ramenem druhého.
Je-li velikost prvního
, kde
koncové rameno prvního z nich je počátečním ramenem druhého.
Je-li velikost prvního 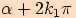 a druhého
a druhého
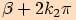 ,
je velikost součtu
,
je velikost součtu 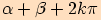 ,
kde
,
kde 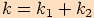 .
.
Rozdílem úhlů 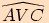 ,
,
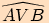 nazýváme úhel
nazýváme úhel 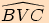 (v uvedeném pořadí).
Je-li velikost prvního
(v uvedeném pořadí).
Je-li velikost prvního 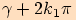 a druhého
a druhého
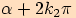 ,
je velikost rozdílu
,
je velikost rozdílu 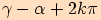 , kde
, kde
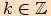 .
.
Příklady
1.
Určete základní velikost orientovaného úhlu, jehož jedna velikost je
a) 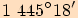

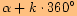 nebo
nebo
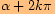 .
. Určíme počet plných otáček.
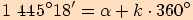



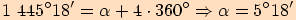

b)
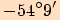

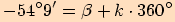

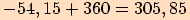

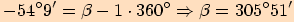

c)
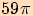

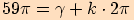

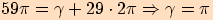

d)
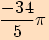

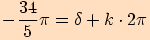

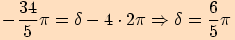

2.
Od 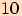 hodin
hodin 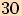 minut se minutová ručička hodinek
otočila o
minut se minutová ručička hodinek
otočila o 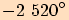 . Kolik hodin potom bylo?
. Kolik hodin potom bylo?

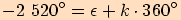


 Ručička se tedy otočila o plných
Ručička se tedy otočila o plných  otáček, tudíž hodinky ukazují
otáček, tudíž hodinky ukazují 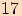 hodin
hodin
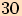 minut.
minut.

>>nahoru<<