Kosinová věta

Pro každý trojúhelník 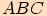, jehož strany mají délky 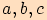a jehož vnitřní úhel proti straně 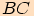má velikost 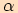, platí .

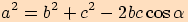Obecný trojúhelník

Poznámka. Jestliže ve vzorci pro kosinou větu přepíšeme symboly stran a úhlů dle cyklické záměny, dostaneme vyjádření pro ostatní strany
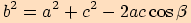, kde úhel 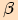je úhel proti straně ,
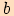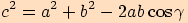, kde úhel 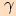je úhel proti straně .

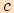Poznámka. Pythagorova věta je vlastně speciálním případem kosinové věty, jestliže je jeden úhel pravý, tzn. .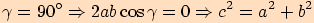

Cyklická záměna

Důkaz

Důkaz provedeme obdobně jako důkaz sinové věty. Také celou situaci rozdělíme na 3 případy a budeme používat bod 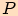, který je patou kolmice spuštěné z bodu 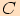na stranu .

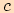1) Úhel 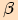je ostrý, tj. .
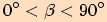Vezměme pravoúhlý trojúhelník 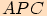. Podle Pythagorovy věty pro jeho strany platí 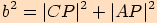. Vyjádříme délku strany , .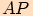
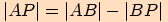Dosadíme-li vztahy získané z trojúhelníku 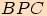, tj. 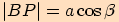, , 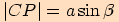do vyjádření délky strany 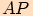, získáme vztah .
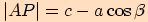Vztahy pro délky stran 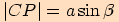a 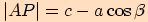dosadíme do první rovnosti, dostáváme .

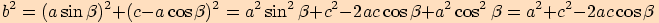2)Úhel 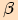je pravý, tj. .
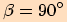Znovu použijeme Pythagorovu větu .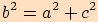
Jelikož je 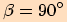, platí 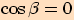(viz Určování hodnot goniometrických funkcí). Tím je dána platnost kosinové věty i v tomto případě, tudíž .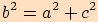

3) Úhel 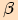je tupý, tj. .
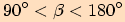Zaměříme se na pravoúhlý trojúhelník 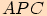. Pomocí Pythagorovy věty vyjádříme 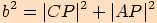V tomto případě platí: .
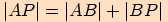Podívejme se teď na trojúhelník 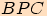a určeme, čemu se rovnají délky stran: 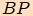a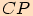

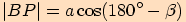
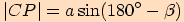
Podle součtových vzorců platí (viz Vzorce pro goniometrické funkce):

Díky součtovým vzorcům upravíme předchozí délky takto:

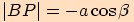
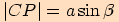
Pro délku strany 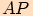platí .
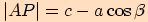Vše potřebné dosadíme do původní rovnice , kterou jsme získali pomocí Pythagorovy věty, a dostaneme 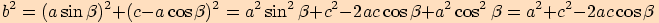. Jde o stejný vztah, který jsme dostali v případě 1) . Tím je důkaz u konce.

>>nahoru<<

Příklady

Vypočítejte délku strany

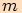v trojúhelníku

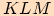, jestliže

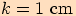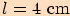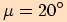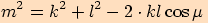
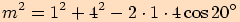
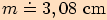
2. Vypočítejte velikosti vnitřní úhlů v trojúhelníku 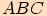, je-li , , .

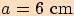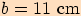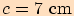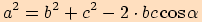
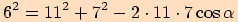
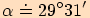
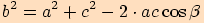
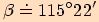
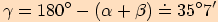
>>nahoru<<