Tečny a normály
Vzájemná poloha přímky a hyperboly
V této kapitole se budeme zabývat vzájemnou polohou hyperboly a přímky. Rozlišíme tři základní situace, které mohou nastat.
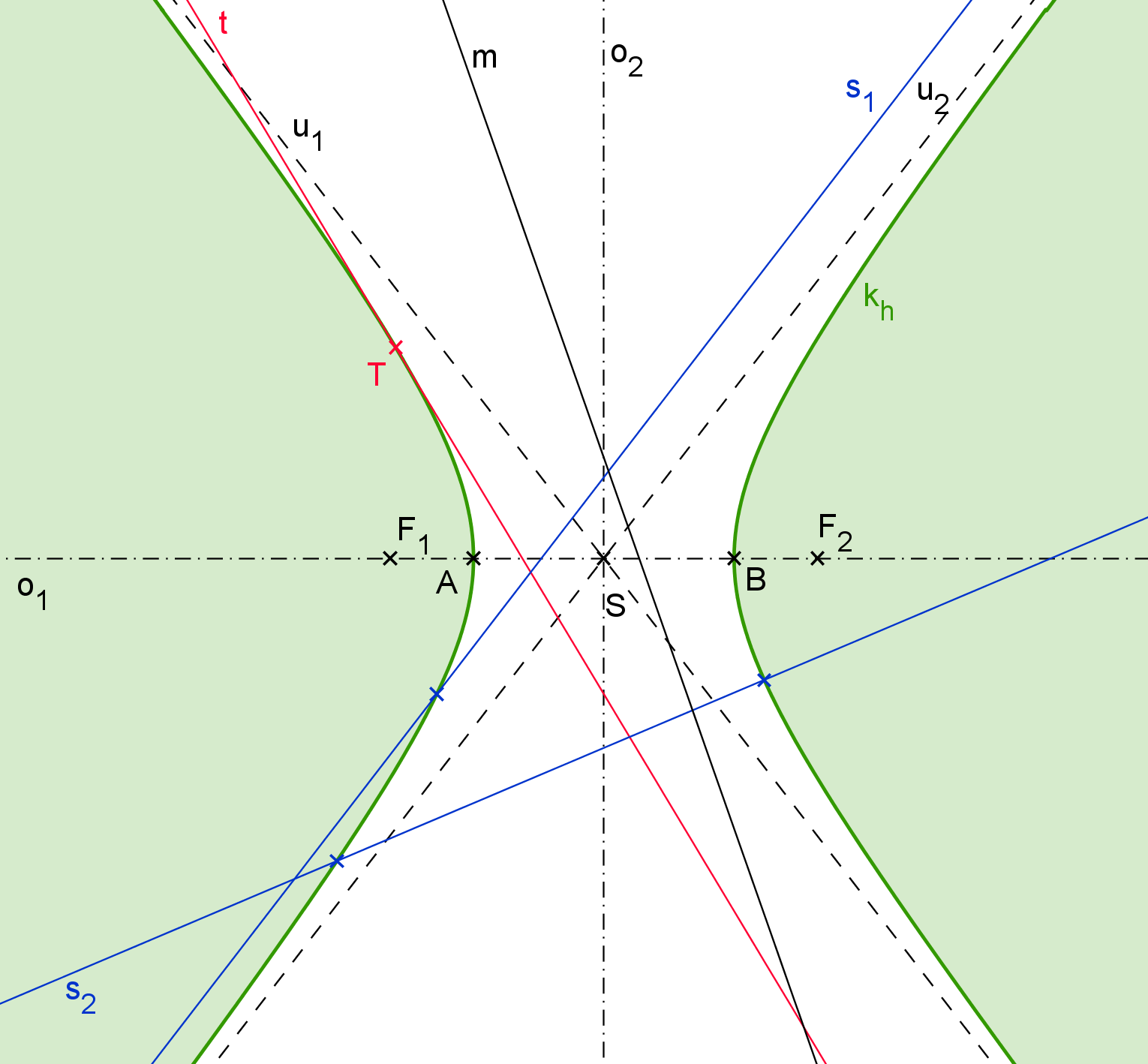
Nechť je v rovině E_2 dána hyperbola k_h. Její větve rozdělují rovinu E_2 na tři disjunktní oblasti: dvě vnitřní oblasti hyperboly oddělené oblastí vnější (viz Základní vlastnosti hyperboly). Přímku nazýváme vnější přímkou hyperboly, jestliže všechny její body leží ve vnější oblasti, tudíž přímka nemá žádný společný bod s hyperbolou. Přímka, která má s hyperbolou společný právě jeden bod a jejíž všechny ostatní body jsou body vnější oblasti, se nazývá tečna hyperboly a společný bod se nazývá bod dotyku. Posledním možností je, že přímka prochází jak vnitřní tak zároveň vnější oblastí hyperboly. V tomto případě hovoříme o sečně hyperboly.
Na obrázku H3.1 představují vnější přímky hyperboly její vedlejší osa o_2 a přímka m. Tečna t v dotykovém bodě T je vyznačena červeně. Modrou barvu zde mají sečny hyperboly, přímky s_1, \, s_2 (hlavní osa o_1 je také sečna). Zde si všimněte, že, i když přímka s_1 má s hyperbolou k_h společný právě jeden bod, není její tečnou. A to, protože zbývající body leží jak ve vnitřní, tak ve vnější oblasti hyperboly.
Obrázek H3.1: Vzájemná poloha přímek a hyperboly (m - vnější přímka; t - tečna; s_1, \, s_2 - sečny)
Tečny a normály hyperboly
Nyní se budeme podrobněji zabývat tečnami hyperboly. Víme, že tečna má pouze jeden společný bod s hyperbolou a že všechny body mino bod dotyku jsou vnějšími body hyperboly. To, že pro každý bod hyperboly existuje pouze jedna tečna, říká následující věta.
Věta H3.1: V každém bodě hyperboly existuje právě jedna tečna.
Nebudeme ji dokazovat, ale dokážeme následující:
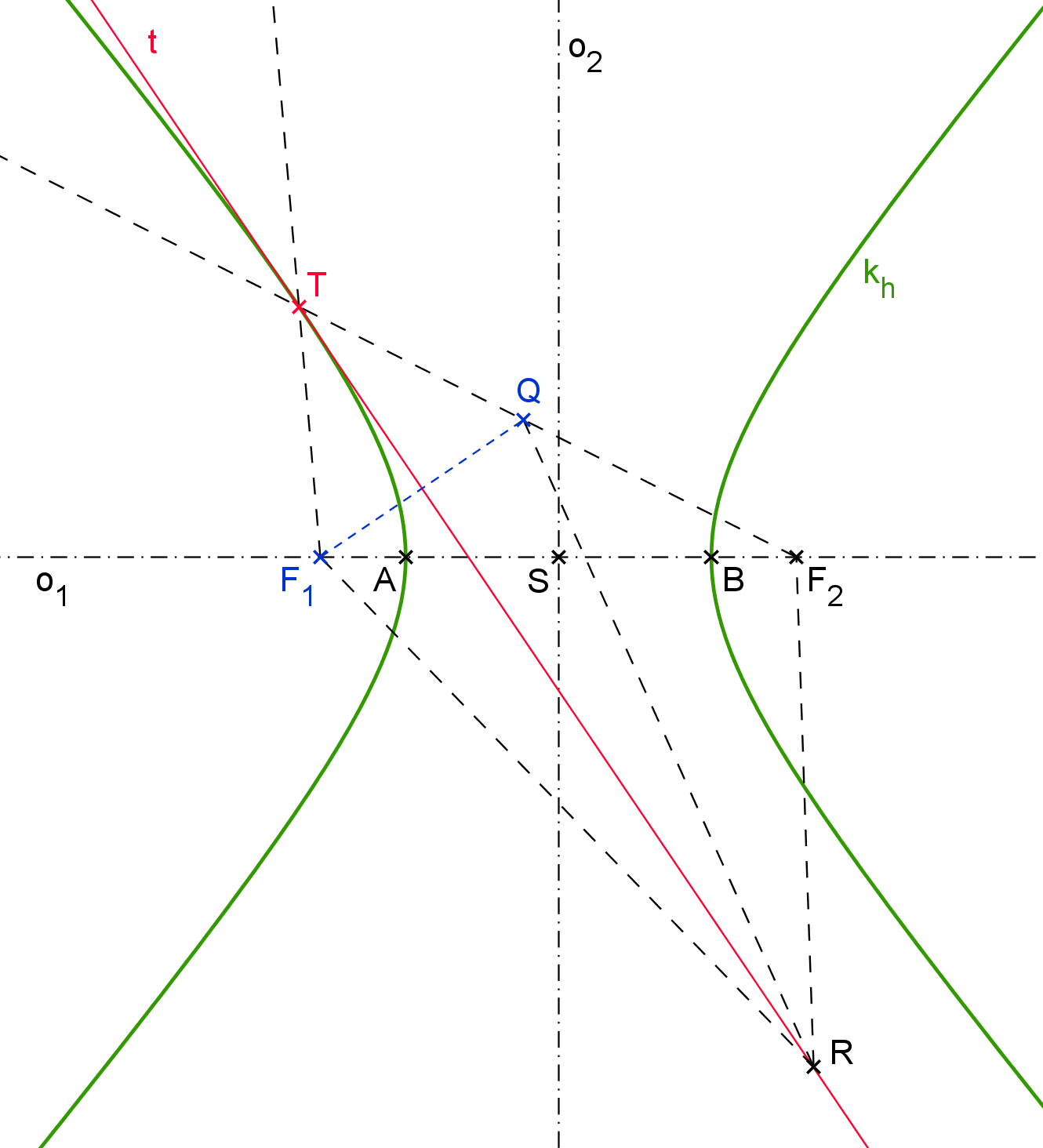
Věta H3.2: Tečna t hyperboly k_h v bodě T je osou vnějších úhlů jeho průvodičů.
Důkaz: (obrázek H3.2) Zvolme libovolně bod T \in k_h. Sestrojme osu t vnějších úhlů průvodičů TF_1, \, TF_2. K jednomu z ohnisek, např. k F_1, najděme souměrně sdružený bod Q podle přímky t. Bod Q je bodem úsečky TF_2. Ze souměrnosti platí: |TQ|=|TF_1|, tedy 2a = ||TF_1| - |TF_2|| = ||TQ| - |TF_2|| = |QF_2|. Zvolme na t libovolný bod R různý od T. Body R, \, F_2, \, Q určují vždy trojúhelník, platí tedy nerovnosti:
|RF_2| + |QF_2| > |RQ|, tedy 2a = |QF_2| > |RQ| - |RF_2|,
|QF_2| + |RQ| > |RF_2|, tedy 2a = |QF_2| > |RF_2| - |RQ|.
Z obou nerovností pak plyne: 2a > ||RQ| - |RF_2||. Protože však |RQ| = |RF_1| (z osové souměrnosti), předchozí nerovnost dává 2a > ||RF_1| - |RF_2||. To znamená, že se jedná o vnější bod hyperboly. Protože bod R byl volen libovolně, tak všechny body kromě bodu T jsou vnějšími body hyperboly. Přímka t nemá s hyperbolou žádný jiný společný bod než právě T. Podle definice je tak přímka t tečnou hyperboly a bod T je bodem dotyku.
Obrázek H3.2: Tečna - osa vnějších úhlů průvodičů; důkaz
Obraťme se nyní k další vlastnosti tečny hyperboly: (citace z: Havlíček [2] str.177)
Věta H3.3: Bod dotyku půlí úsečku vyťatou na příslušné tečně hyperboly jejími asymptotami.
Věta jinými slovy říká, že bod dotyku T je středem úsečky XY, kde body X, \, Y jsou průsečíky tečny t s asymptotami u_1, \, u_2 hyperboly. (Pozn.: tato věta vychází z vlastností hyperboly v projektivní geometrii. Není v kompetenci této práce zasvětit čtenáře do projektivních vlastností kuželoseček, ale pro významnost je věta uvedena.)
Důkaz: Zobecněním věty H3.3 je věta H3.5, která je uvedena níže v podkapitole Sečny hyperboly. Důkaz tedy bude obdobný důkazu věty H3.5.
Pro názornost je zde k dispozici aplet H3.1. Pohybem bodu dotyku T po hyperbole budete moci měnit tečnu t hyperboly. Ovšem všímejte si, že je vzdálenost bodu T od výše zmíněných bodů X, \, Y stejná, tedy: |XT|=|YT|.
Aplet H3.1: Bod dotyku T půlí úsečku XY.
Zvláštními a významnými sečnami hyperboly jsou ty, které jsou kolmé na tečny hyperboly v příslušných bodech dotyku. Nazývají se normály hyperboly.
Pro normálu platí, jako snadný důsledek věty H3.2, následující:
Věta H3.4: Normála hyperboly půlí vnitřní úhly průvodičů bodu, v němž byla sestrojena.
Z pohledu kinematické geometrie tečny hyperboly obalují hyperbolu. Hyperbola je tedy obalovou křivkou svých tečen. Obalová křivka normál hyperboly se nazývá evoluta hyperboly. Je to množina všech středů křivosti dané hyperboly. Vrcholy evoluty jsou středy křivosti oskulačních kružnic ve vrcholech hyperboly (více viz kapitola Oskulační kružnice hyperboly). Na rozdíl od evoluty elipsy má evoluta hyperboly dvě větve, o čemž se můžete přesvědčit v apletu H3.2, kde je část evoluty hyperboly zobrazena. Pohybujte zde dotykovým bodem T po větvích hyperboly k_h. Sledujte přitom pohyb tečny t po hyperbole a pohyb normály n po větvích evoluty hyperboly (ta je vyznačena čárkovaně modrou barvou).
Aplet H3.2: Evoluta hyperboly - obalová křivka normál hyperboly
Sečny hyperboly
Budeme-li se bavit o obecné sečně hyperboly, vznikají zde úseky vyťaté hyperbolou a jejími asymptotami, které jsou shodné. Sečna s má následující vlastnost: (citace z: Drábek, Harant, Setzer [1] str. 62)
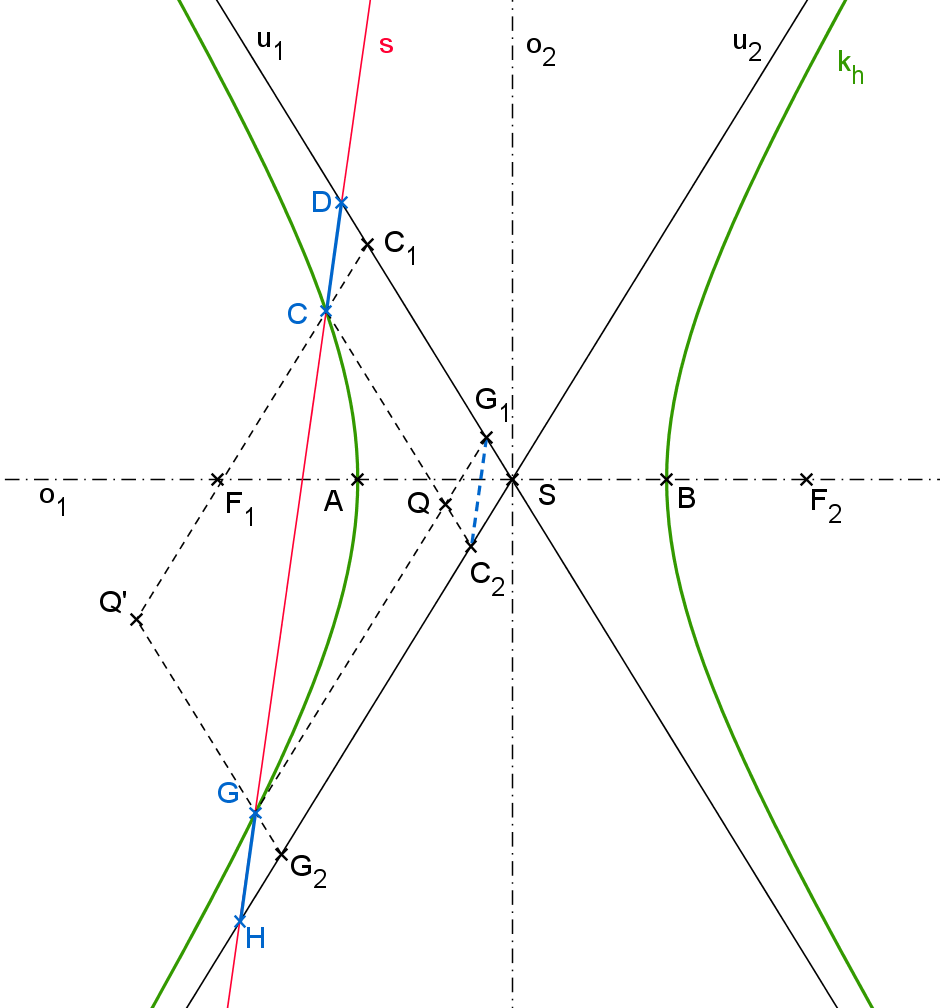
Věta H3.5: Úseky na sečně s hyperboly k_h měřené od bodu hyperboly k jedné asymptotě u_1 a od druhého bodu hyperboly k druhé asymptotě u_2 jsou stejně velké.
Zobecnění této věty již zaznělo výše - věta H3.3. Opět je to věta, která vychází z projektivních vlastností hyperboly. Ovšem pro její důležitost a výhodné využití při konstrukcích hyperboly, je zde uvedena.
Důkaz: (obrázek H3.3) Zvolme libovolně sečnu s hyperboly k_h. Průsečíky sečny s hyperbolou označme C, \, G, průsečíky s asymptotami u_1, \, u_2 označíme D, \, H.
Každým z bodů C, \, G veďme dvě rovnoběžky, a to s asymptotami u_1, \, u_2, Průsečíky rovnoběžek s asymptotami označme C_1, \, C_2,\, G_1,\, G_2 a Q, \, Q' průsečíky rovnoběžek samotných (viz obrázek H3.4).
Důkaz plyne ze stejnolehlosti rovnoběžníků QCQ'G a QC_2SG_1 pro střed stejnolehlosti Q. Z toho vyplývá, že CG \, || \, C_2G_1. Tedy sečna s je rovnoběžná s C_2G_1. Pak zde vznikají shodné trojúhelníky: SG_1C_2, C_1DC, G_2GH. Z tohoto faktu plyne: |DC| =|GH|.
Obrázek H3.3: Úseky na sečně hyperboly
V apletu H3.3 měňte polohu sečny s pomocí červených bodů X, \, Y. Na levé straně apletu přitom sledujte délky zmiňovaných úseků, jsou shodné.
Aplet H3.3: Shodné úseky na sečně hyperboly