Základní vlastnosti
Základní vlastnosti hyperboly
V této kapitole odkryjeme několik základních vlastností, které hyperbola má. Budeme se zabývat opravdu jen základními vlastnostmi. Rozšířením této kapitoly bude kapitola Tečny a normály hyperboly a Ohniskové vlastnosti hyperboly, jež bude navazovat na informace a látku probranou právě zde.
Základní důležitou vlastností hyperboly je, že libovolný bod na ní ležící má konstantní absolutní hodnotu rozdílu vzdáleností od ohnisek rovnu 2a > 0. Na tom je samozřejmě postavená definice hyperboly. Nicméně z této vlastnosti vyplývá několik dalších.
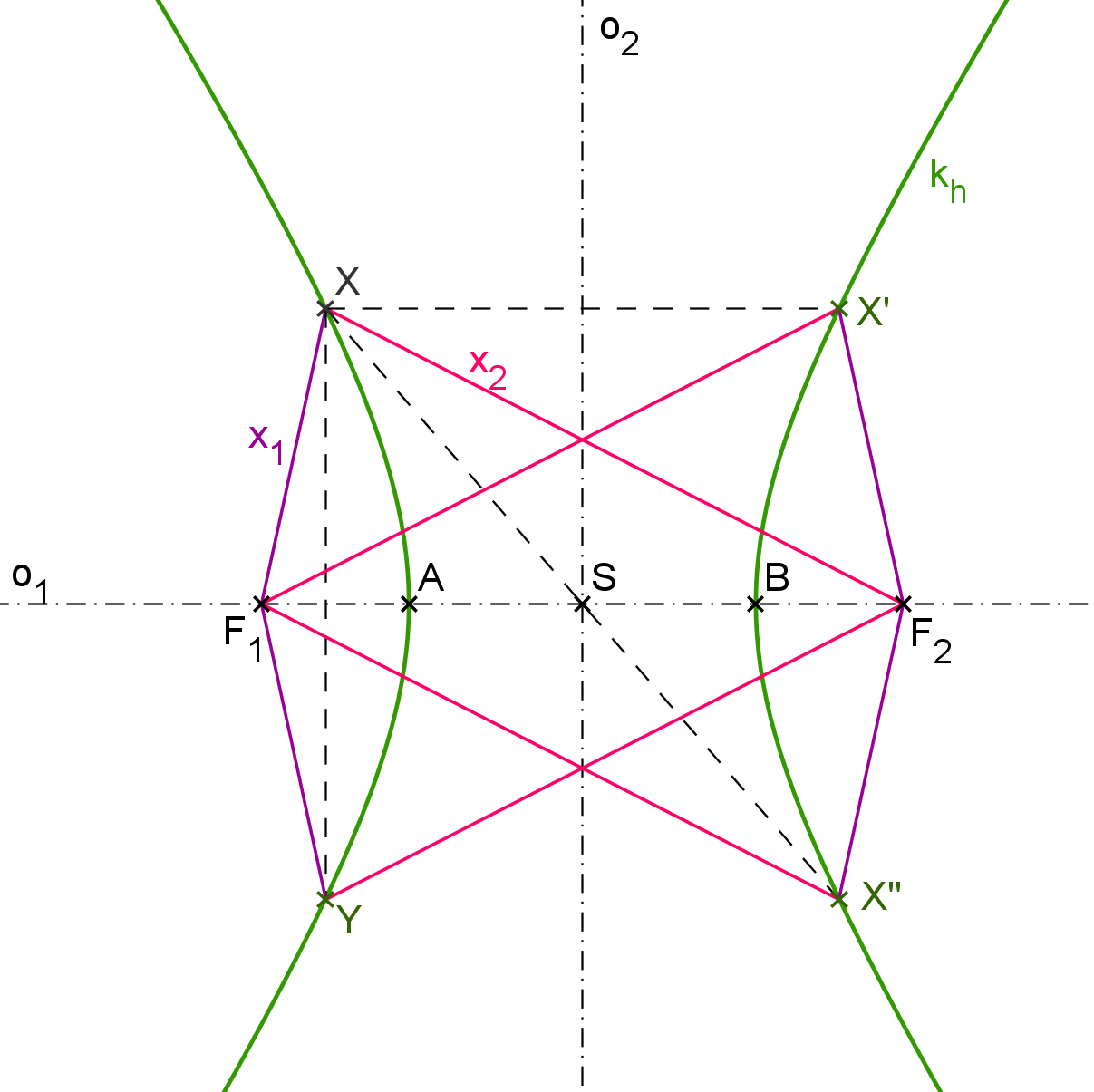
Zvolme nyní libovolně bod X \in k_h. Zvolme ho tak, aby ležel "nad" hlavní osou hyperboly. Označme x_1 vzdálenost bodu X od ohniska F_1 a x_2 vzdálenost bodu X od druhého ohniska F_2. Potom zajisté body X' a X'', pro které platí: |X'F_1| = |X''F_1| = x_2, |X'F_2| = |X''F_2| = x_1, budou také součástí hyperboly (bod X' leží "nad" o_1, bod X'' "pod" o_1). Navíc platí, že bod X' je s bodem X osově souměrný podle vedlejší osy o_2. Protože bod X byl zvolen libovolně, mohli jsme si vybrat jakýkoliv bod hyperboly, můžeme konstatovat, že hyperbola je osově souměrná podle vedlejší osy o_2. Bod X'' je středově souměrný s bodem X podle středu S. Můžeme tedy opět říci, že hyperbola je středově souměrná podle středu S.
Vraťme se ještě ke zvolenému bodu X. Bod, jenž má vzdálenost x_1 od ohniska F_1 a vzdálenost x_2 od druhého ohniska F_2 existuje na hyperbole ještě jeden (leží "pod" hlavní osou). A zřejmě platí, že tento bod je osově souměrný s původním bodem X podle hlavní osy o_1. Hyperbola je tedy také osově souměrná podle hlavní osy o_1.
Vše popisované je znázorněno na obrázku H2.1.
Obrázek H2.1: Souměrnosti hyperboly
Pokud bychom vše měli shrnout, můžeme vyslovit tvrzení:
Věta H2.1: Hyperbola je souměrná podle dvou na sebe kolmých os. Jedná se o hlavní a vedlejší osu hyperboly. Je také souměrná podle jejich průsečíku, středu.
V apletu H2.1 si můžete vyzkoušet, výše popsané vlastnosti. Budete-li pohybovat body X_1, X_2, X_3 po hyperbole, budou se též body X'_1, X'_2, X'_3 souměrně sdružené pohybovat po hyperbole.
Aplet H2.1: Souměrnosti hyperboly
Už z předešlé kapitoly Definice hyperboly víme, že i přestože na hyperbole nenalezneme žádné vedlejší vrcholy, je zde definována délka vedlejší poloosy b. Je vyjádřena jako délka odvěsny AU_1 (resp. BU_2) v pravoúhlém trojúhelníku SAU_1 (resp. SBU_2) s pravým úhlem při vrcholu A (resp. B), kde U_1 \in u_1 (U_2 \in u_2). Délka |SA| = |SB| je délka hlavní poloosy a a délka |SU_1| = |SU_2| představuje excentricitu hyperboly, tedy e. Z pravoúhlého trojúhelníku SAU_1, kterému se také říká charakteristický trojúhelník hyperboly, se stranami délek: |SA| = a, \, |AU_1| = b, \, |U_1S| = e vyplývá vztah: e^2 = a^2 + b^2 (Pythagorova věta).
Z předchozího vyplývá, že odchylka \alpha asymptot u_1, \, u_2 od hlavní osy o_1 hyperboly taktéž závisí na velikosti hlavní a vedlejší poloosy. Z charakteristického trojúhelníku platí: tg \, \alpha = \frac {b} {a}.
Věta H2.2:
Pro délku hlavní a vedlejší poloosy hyperboly (a, b) a excentricitu e platí vztah (Pythagorova věta): e^2 = a^2 + b^2.
Asymptoty u_1, \, u_2 hyperboly mají odchylku \alpha od hlavní osy o_1, pro niž platí: tg \, \alpha = \frac {b} {a}.
Charakteristický trojúhelník udává tvar hyperboly, což si můžete v apletu H2.2 vyzkoušet. Zde je zobrazen charakteristický trojúhelník ASU_1. Někdy se ovšem můžete setkat s pojmem charakteristický obdélník hyperboly. Jedná se o obdélník o stranách délek 2a a 2b. Vrcholy tvoří body U_1, \, U_2, \, U_3, \, U_4, které jsou průsečíky přímek kolmých k hlavní ose o_1 vedených z vrcholů A,\, B a asymptot u_1, \, u_2 hyperboly. Úhlopříčky takového charakteristického obdélníku mají délku 2e a protínají se ve středu S hyperboly (viz aplet H2.2). Měňte v apletu polohu vrcholu A nebo pohybujte jedním z ohnisek (F_1, \, F_2) po hlavní ose o_1 a pozorujte jak se mění tvar hyperboly.
Aplet H2.2: Charakteristický trojúhelník a tvar hyperboly
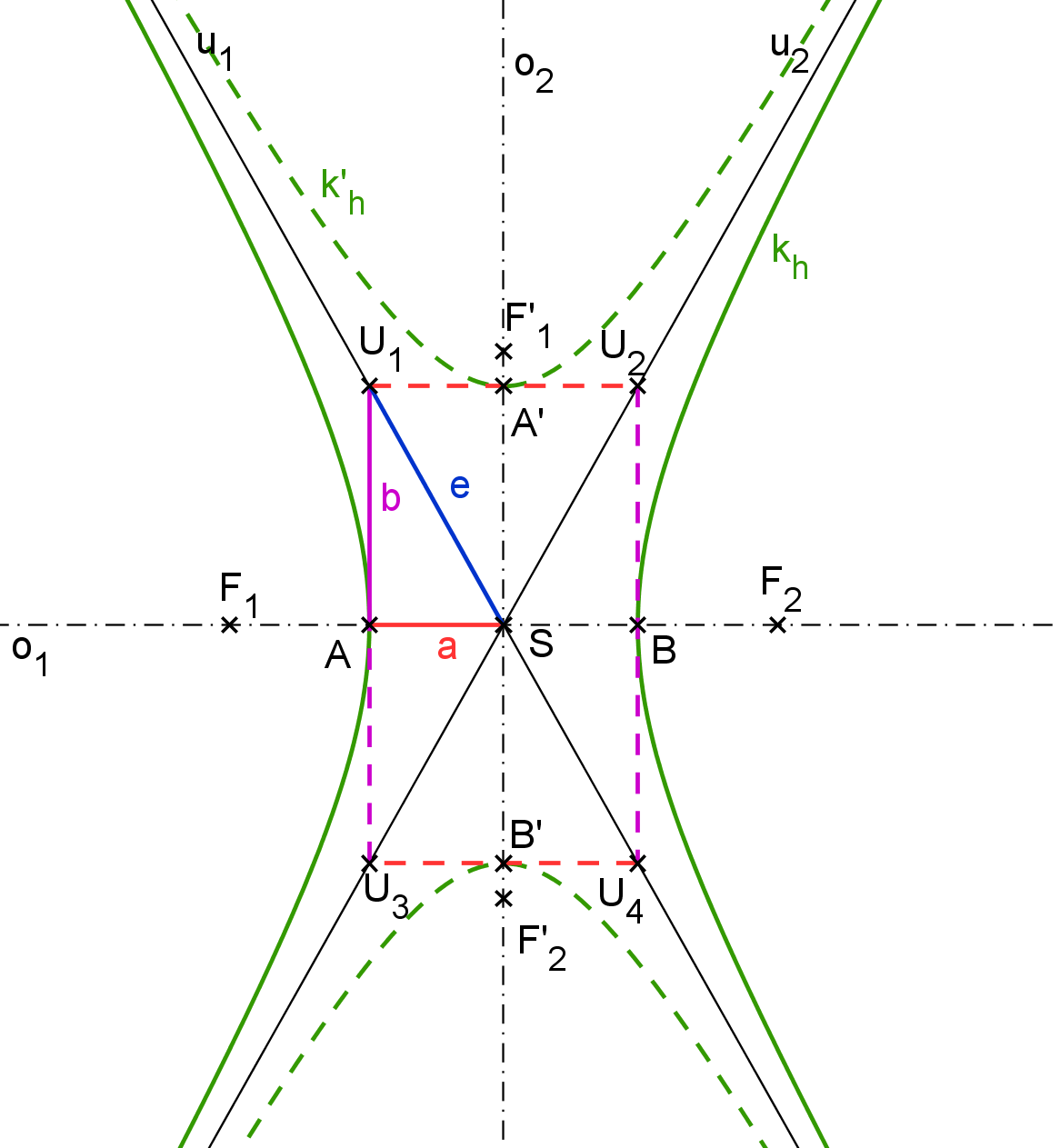
Ke každé hyperbole k_h existuje hyperbola k'_h (viz obrázek H2.2), která má tentýž charakteristický obdélník, nazývá se doplňková hyperbola. Doplňková hyperbola má tedy stejnou hodnotu excentricity e, délka její hlavní poloosy je rovna b a délka vedlejší poloosy rovna a. Asymptoty hyperboly k_h a její doplňkové hyperboly k'_h jsou ty samé přímky u_1, \, u_2.
Obrázek H2.2: Doplňková hyperbola
Pro průvodiče MF_1, MF_2 libovolného bodu M roviny E_2 může nastat jeden ze tří případů:
a) ||MF_1| - |MF_2|| < 2a ,
b) ||MF_1| - |MF_2|| = 2a,
c) ||MF_1| - |MF_2|| > 2a.
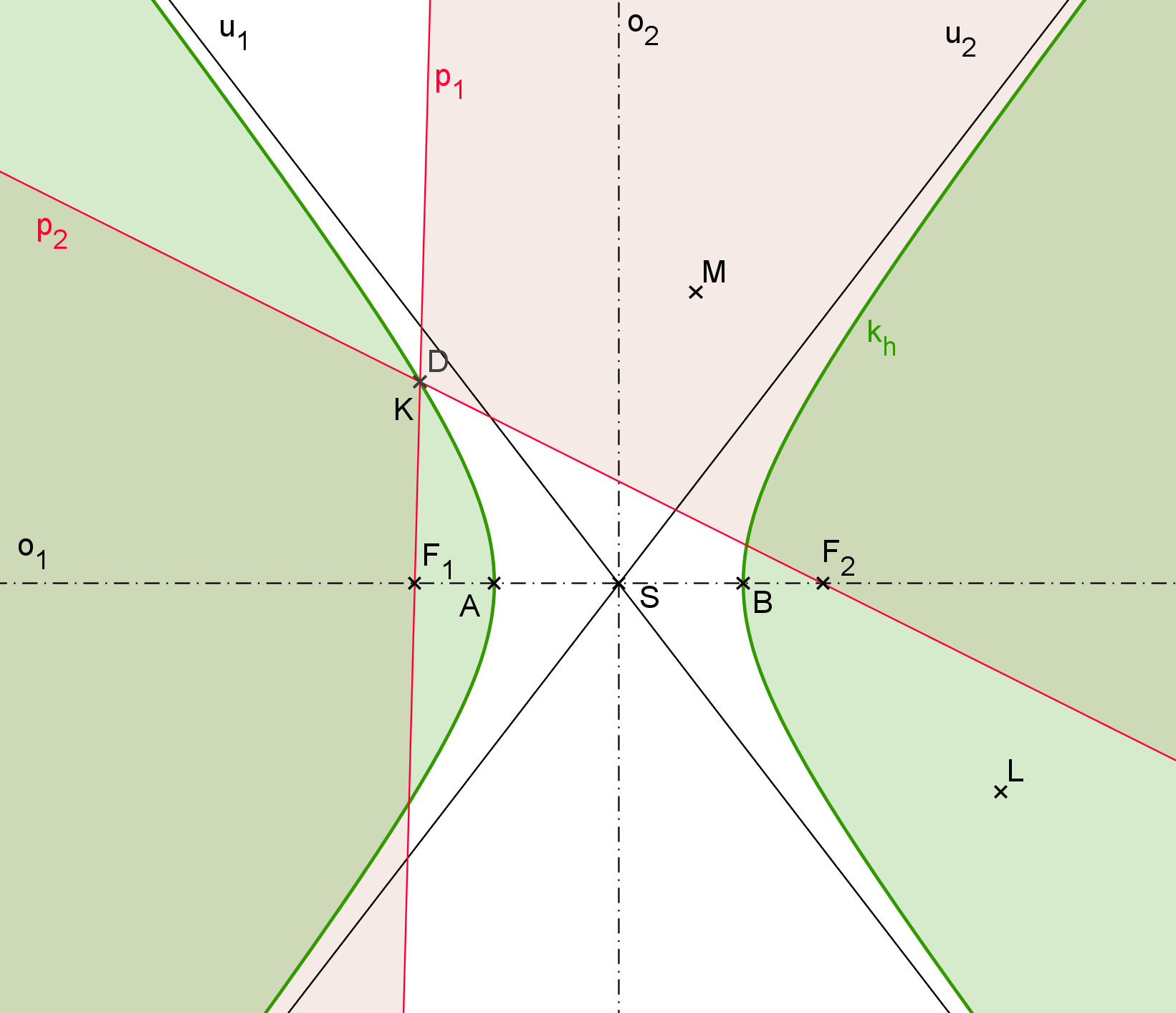
Body, pro které platí b) jsou jistě body hyperboly. V případě a) mluvíme o vnějších bodech hyperboly, v případě c) o vnitřních bodech. Větve hyperboly rozdělují rovinu E_2 na tři disjunktní oblasti, přičemž vnitřní body hyperboly leží právě ve dvou z nich. Ohniska jsou vnitřní body, ale střed je vnějším bodem. Na obrázku H2.3 jsou zeleně vybarveny vnitřní části hyperboly, vnější část je bíle. Bod M splňuje podmínku a), je tedy vnějším bodem. Bod K splňuje b) a je bodem hyperboly. Pro bod L platí c), je vnitřním bodem hyperboly.
Hyperbola a její vnitřní body tvoří konkávní oblast. Jinými slovy, je to oblast, ve které existují body, jejichž spojnice (úsečka) prochází i vnější oblastí. (Např. pokud zvolíme ohniska F_1, \, F_2, obě sice leží ve vnitřní oblasti, ale jejich spojnice prochází i vnější oblastí.)
Na obrázku H2.3 jsou ještě vyznačeny průvodiče bodu K. Ze čtyř úhlů, které tvoří průvodiče tohoto bodu, vždy jeden obsahuje S - střed hyperboly. Úhel tvořený polopřímkami KF_1, KF_2, který obsahuje střed, a příslušný vrcholový úhel se nazývají vnější úhly průvodičů. Úhly vedlejší k vnějším úhlům se nazývají vnitřní úhly průvodičů bodu hyperboly. Na obrázku jsou vnitřní úhly vyznačeny barevně.
Obrázek H2.3: Vnitřní oblast a průvodiče hyperboly