Tečny a normály
Vzájemná poloha přímky a elipsy
Nechť je dána v rovině E_2 elipsa k_e. Budeme se nyní zabývat, jaké druhy přímek ve vztahu k elipse mohou v rovině existovat.
Z kapitoly Základní vlastnosti elipsy víme, že elipsa rozděluje rovinu E_2 na dvě disjunktní oblasti: vnitřní a vnější oblast. Je patrno, že přímka buď nemá s elipsou žádný společný bod (a všechny její body jsou vnějšími body elipsy), nebo má s ní společný právě jeden bod (a všechny ostatní jsou vnější), nebo právě dva různé body. (čerpáno z: Urban [13] str.36)
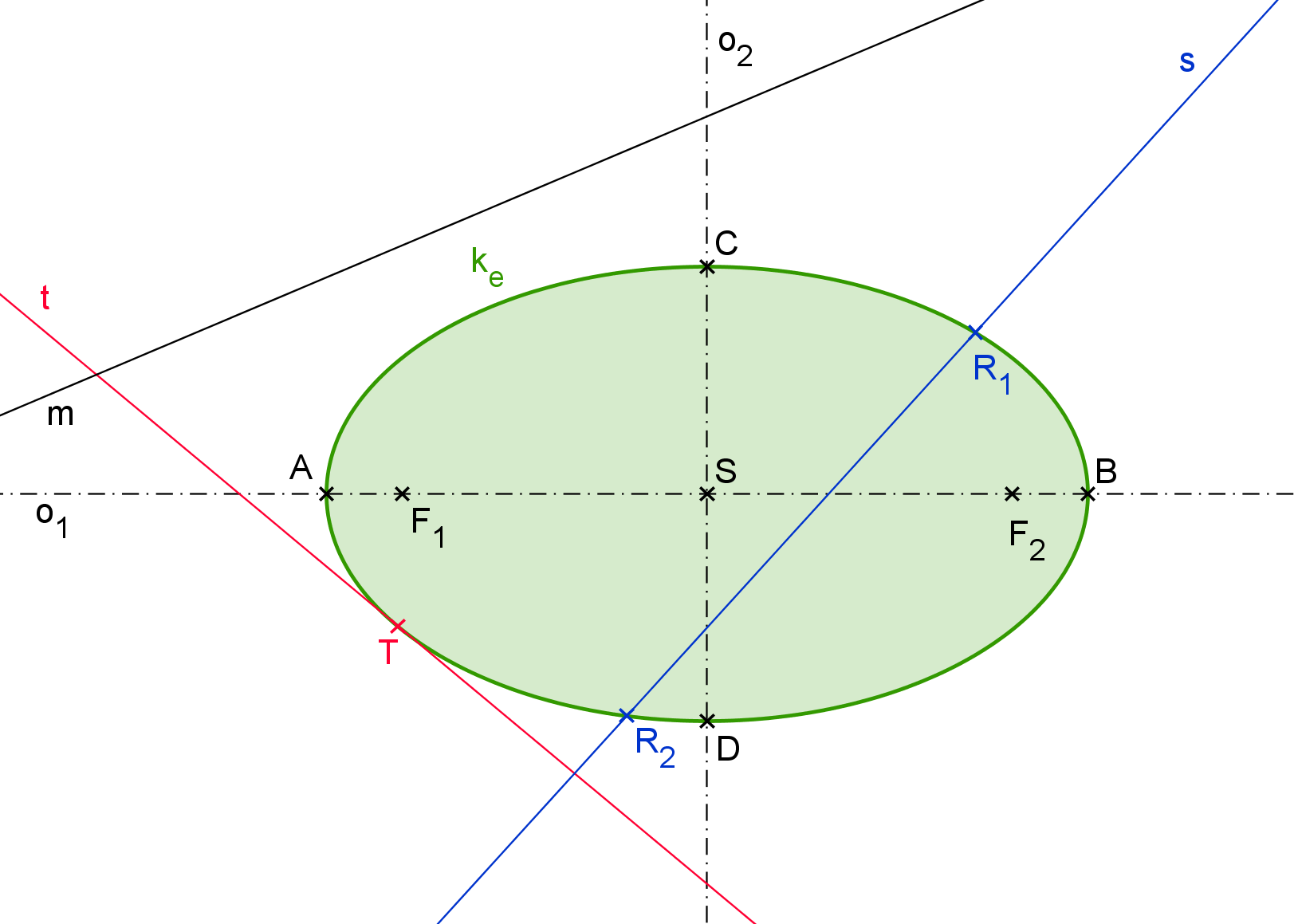
V prvním případě hovoříme o tzv. vnější přímce elipsy (někdy také nesečna elipsy). Na obrázku E3.1 je přímka m vnější přímkou. Červeně zobrazená přímka t má s elipsou k_e společný jediný bod, bod T. Nazýváme ji tečna elipsy, společnému bodu se říká bod dotyku. Posledním případem je přímka, která prochází vnitřní částí elipsy a má s elipsou společné právě dva různé body. Na obrázku E3.1 je to přímka s, má modrou barvu a obecně se nazývá sečna elipsy. (Speciálními sečnami jsou tzv. průměry elipsy. Více o nich je v kapitole Průměry elipsy)
Obrázek E3.1: Vzájemná poloha přímek a elipsy (m - vnější přímka; t - tečna; s - sečna)
Tečny a normály elipsy
Budeme se nyní podrobněji zabývat tečnami elipsy. Víme, že tečna má pouze jeden společný bod s elipsou. Opak, že pro každý bod elipsy existuje pouze jedna tečna, říká následující věta.
Věta E3.1: V každém bodě elipsy existuje právě jedna tečna.
Nebudeme ji dokazovat, ale dokážeme následující:
Věta E3.2: Tečna t elipsy k_e v bodě T je osou vnějších úhlů jeho průvodičů.
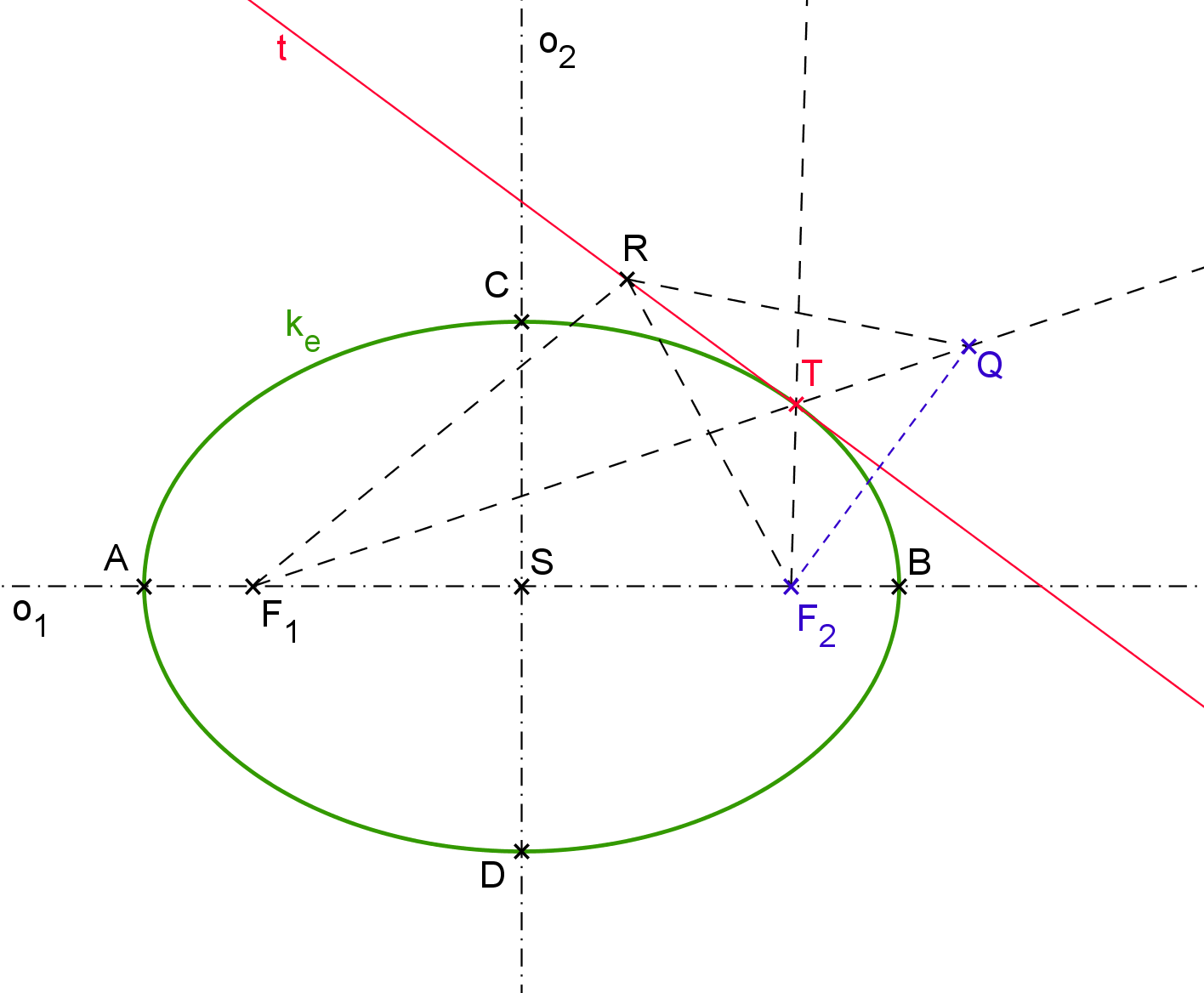
Důkaz: (obrázek E3.2) Zvolme libovolně bod T \in k_e. Sestrojme osu t vnějších úhlů průvodičů TF_1, \, TF_2. K jednomu z ohnisek, např. k F_2, najděme souměrně sdružený bod Q podle přímky t. Bod Q je bodem polopřímky opačné k polopřímce TF_1. Ze souměrnosti platí: |TQ|=|TF_2|, tedy |F_1Q| = |F_1T| + |TQ| = |F_1T| + |F_2T| = 2a. Zvolme na t libovolný bod R různý od T. Body R, \, F_1, \, Q určují vždy trojúhelník, platí tedy nerovnost: |RF_1| + |RQ| > |F_1Q| = 2a. Protože však |RQ| = |RF_2| (z osové souměrnosti), předchozí nerovnost dává |RF_1| + |RF_2| > 2a. To znamená, že všechny body přímky t kromě bodu T jsou vnějšími body elipsy, přímka t nemá s elipsou žádný jiný společný bod než právě T. Podle definice je tak přímka t tečnou elipsy a bod T je bodem dotyku. (čerpáno z: Urban [13] str.36)
Obrázek E3.2: Tečna - osa vnějších úhlů průvodičů; důkaz
Zvláštními a významnými sečnami elipsy jsou ty, které jsou kolmé na tečny elipsy v příslušných bodech dotyku. Nazývají se normály elipsy. Význam normál spočívá např. v některých konstrukcích elipsy, kde se pomocí nich dohledávají jednotlivé body elipsy.
Pro normálu platí, jako snadný důsledek předchozí věty, následující:
Věta E3.3: Normála elipsy půlí vnitřní úhly průvodičů bodu, v němž byla sestrojena.
Z pohledu kinematické geometrie tečny elipsy obalují elipsu. Elipsa je tedy obalovou křivkou svých tečen. Obalová křivka normál elipsy se nazývá evoluta elipsy. Je to množina všech středů křivosti dané elipsy. Vrcholy evoluty jsou středy křivosti oskulačních kružnic ve vrcholech elipsy (více viz kapitola Oskulační kružnice elipsy). Evoluta elipsy je rovinná křivka, která se nazývá asteroida. Pomocí trojúhelníkové konstrukce lze přesně dohledat nejen normálu, ale i střed křivosti v bodě - bod evoluty (trojúhelníková konstrukce viz kapitola Konstrukce elipsy).
V apletu E3.1 pohybujte dotykovým bodem T po elipse k_e. Sledujte přitom pohyb tečny t po elipse a pohyb normály n po evolutě elipsy (ta je vyznačena čárkovaně modrou barvou).
Aplet E3.1: Evoluta elipsy - obalová křivka normál elipsy