Tečny a normály
Vzájemná poloha přímky a paraboly
V této kapitole se budeme zabývat vzájemnou polohou paraboly a přímky. Stejně, jak tomu je u elipsy a hyperboly, tak i u paraboly rozlišíme tři základní situace, které mohou nastat.
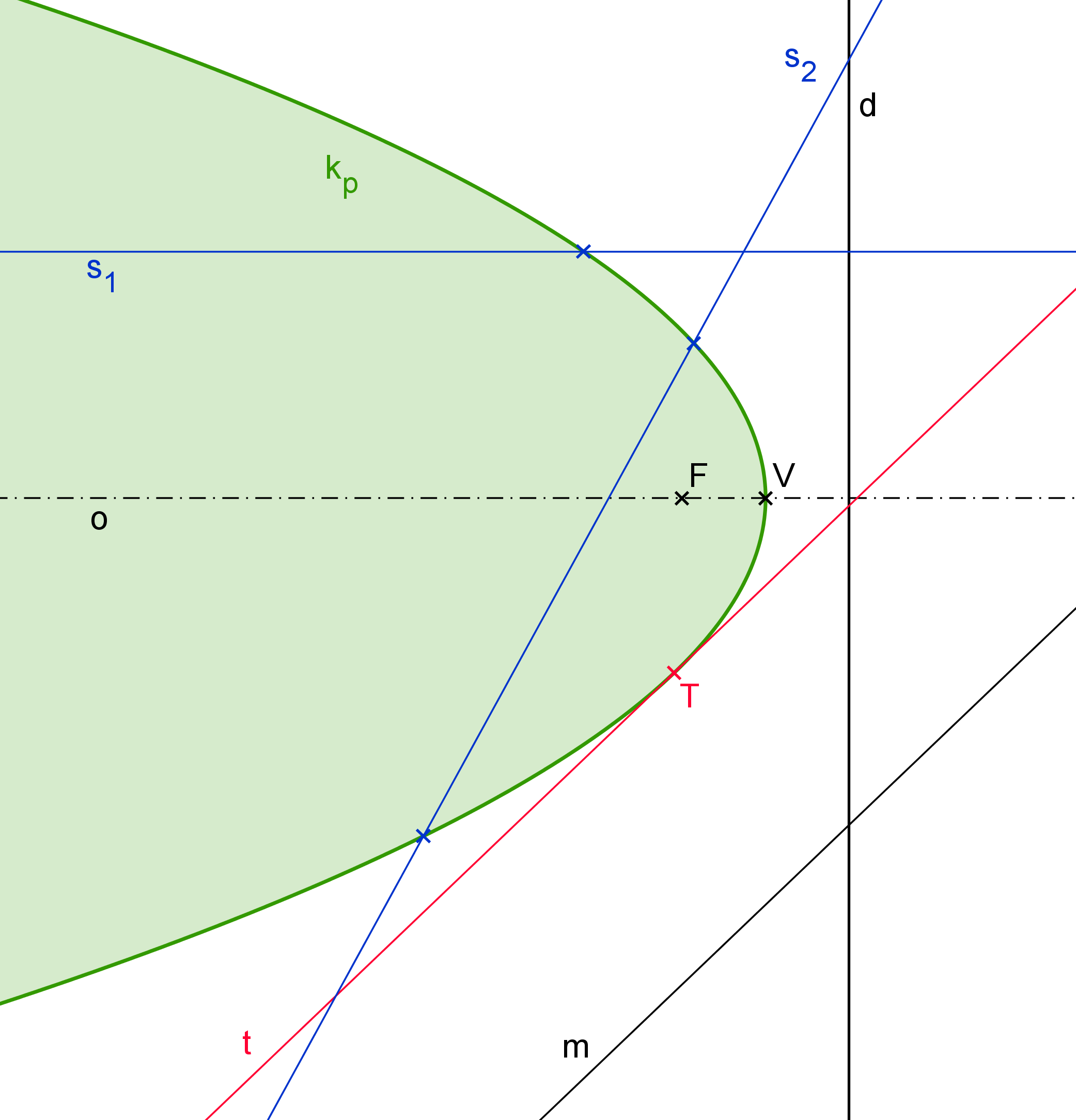
Nechť je v rovině E_2 dána parabola k_p. Ta rozděluje rovinu E_2 na dvě disjunktní oblasti: vnitřní a vnější (viz Základní vlastnosti paraboly). O vzájemné poloze přímky a paraboly k_p můžeme zaprvé říci, že přímka nemá s parabolou žádný společný bod. Leží tedy celá ve vnější oblasti paraboly a nazývá se vnější přímka paraboly. Na obrázku P3.1 představuje takovou přímku přímka m nebo také řídicí přímka d. Další možností je, že přímka má s parabolou společný právě jeden bod T a zároveň její všechny ostatní body (mimo bod T) leží ve vnější oblasti. Jedná se o tečnu paraboly. Nejčastěji ji značíme t (stejně, jak je tomu na obrázku P3.1) a bod T nazýváme bod dotyku. Posledním případem je přímka, která prochází vnitřní částí paraboly. Na obrázku P3.1 jsou to přímky s_1, \, s_2, mají modrou barvu a obecně se nazývají sečny paraboly. Sečny mohou mít jeden nebo dva společné body s parabolou, jak je z obrázku zřejmé.
Obrázek P3.1: Vzájemná poloha přímek a paraboly (m - vnější přímka; t - tečna; s_1, \, s_2 - sečny)
Tečny a normály paraboly
Budeme se nyní podrobněji zabývat tečnami paraboly. Pokud zrekapitulujeme definici tečny z předchozí podkapitoly, tak tečna paraboly je přímka, která má pouze jeden společný bod s parabolou a všechny body mino bod dotyku jsou vnějšími body paraboly. Další vlastnost dává následující věta.
Věta P3.1: V každém bodě paraboly existuje právě jedna tečna.
Nebudeme ji dokazovat, ale dokážeme následující:
Věta P3.2: Tečna t paraboly k_p v bodě T je osou vnějších úhlů jeho průvodičů.
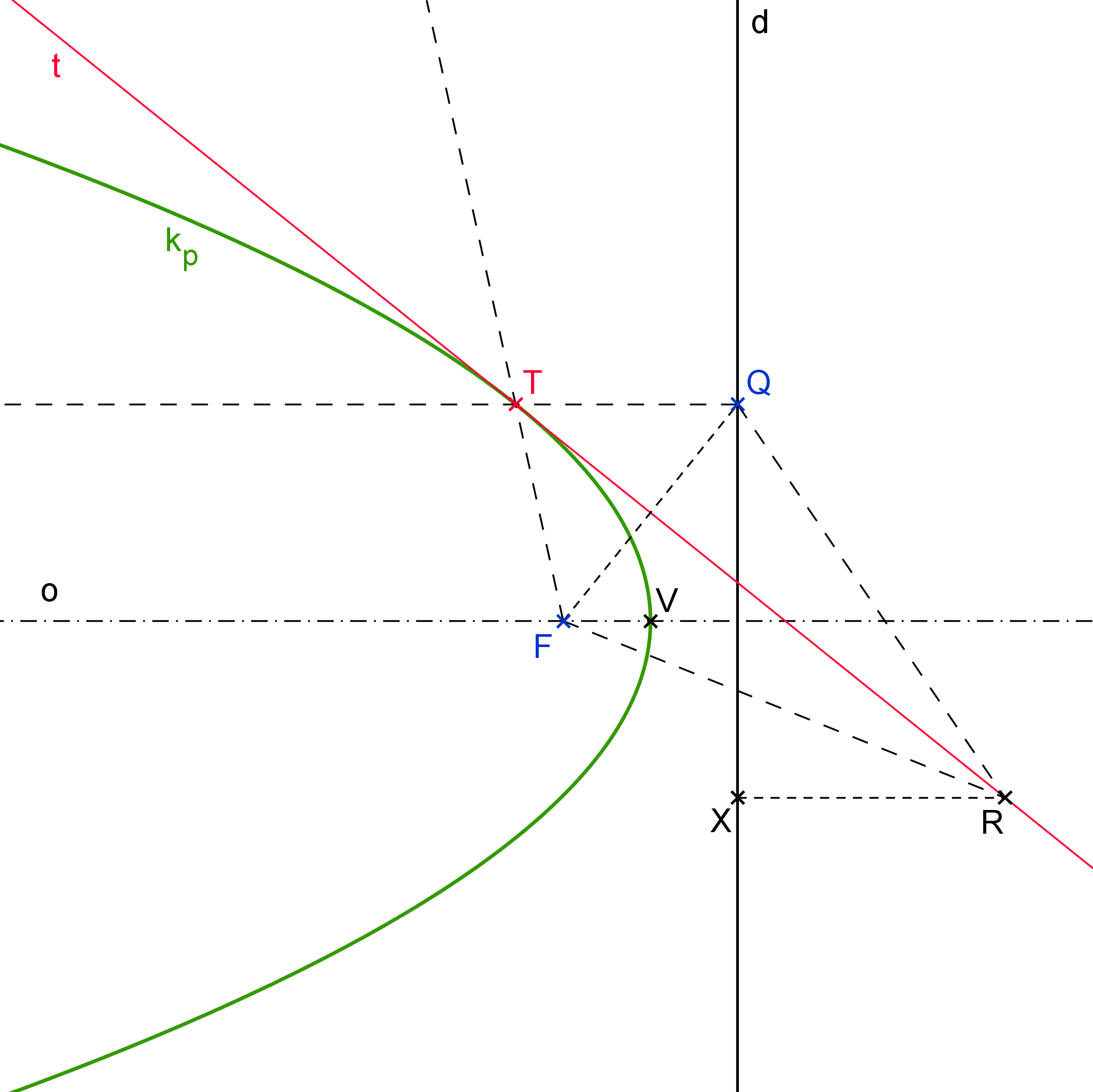
Důkaz: (obrázek P3.2) Zvolme libovolně bod T \in k_p. Sestrojme osu t vnějších úhlů průvodičů bodu T. Nechť Q je pata kolmice z T na d. Podle definice paraboly platí: |TF|=|TQ|. A protože t je osa úhlu FTQ, je bod Q souměrně sdružený s ohniskem F podle přímky t. Tedy pro libovolný bod R \in t je |RF| = |RQ|. Zvolme bod R mimo bod dotyku T a sestrojme patu X kolmice z R na řídicí přímku d. Protože body X a Q jsou různé, je |RQ| > |RX|, a tedy |RF| > |RX|. Z toho plyne, že každý takový bod (mimo bod T) je vnějším bodem paraboly. Přímka t je podle definice tečnou paraboly.
Obrázek P3.2: Tečna - osa vnějších úhlů průvodičů; důkaz
Důležitými sečnami paraboly jsou ty, které jsou kolmé na tečny paraboly v příslušných bodech dotyku. Nazývají se normály paraboly. (Na normálách leží středy příslušných oskulačních kružnic.)
Pro normálu platí, jako snadný důsledek předchozí věty, následující:
Věta P3.3: Normála paraboly půlí vnitřní úhly průvodičů bodu, v němž byla sestrojena.
Pokud se na parabolu budeme dívat z pohledu kinematické geometrie, můžeme konstatovat, že tečny paraboly parabolu v podstatě obalují. Parabola je tedy obalovou křivkou svých tečen. Obdobně existuje i obalová křivka normál paraboly. Nazývá se evoluta paraboly. Je to rovinná křivka, množina všech středů křivosti dané paraboly. Vrchol evoluty je střed křivosti oskulační kružnice ve vrcholu paraboly (více viz kapitola Oskulační kružnice paraboly).
V apletu P3.1 pohybujte dotykovým bodem T po parabole k_p. Sledujte přitom pohyb tečny t po parabole a pohyb normály n po evolutě paraboly (ta je vyznačena čárkovaně modrou barvou).
Aplet P3.1: Evoluta paraboly - obalová křivka normál paraboly