Osy úhlů
Osa úhlu BAC je polopřímka, která rozděluje 
BAC na dva úhly stejné velikosti. Pro její body platí, že jejich vzdálenost od přímek (popř. stran) AB a AC je stejná.
Osa úhlu 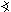BAC v rovině ρ jako množina bodů:
kde zápisem d(X,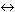
AB) rozumíme vzdálenost bodu X od přímky 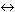AB, tedy od paty kolmice procházející bodem X na přímku 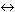AB.
BAC v rovině ρ jako množina bodů:{X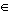
ρ; d(X, 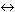AB) = d(X, 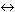AC)}
ρ; d(X, AB) = d(X, AC)}kde zápisem d(X,
AB) rozumíme vzdálenost bodu X od přímky AB, tedy od paty kolmice procházející bodem X na přímku AB.
Osy úhlů trojúhelníku mají jeden společný bod Sv.
Pro dvě osy existuje jeden průsečík, pro který platí, že je stejně vzdálený od všech tří stran, tedy jím musí procházet i osa třetí.
Kružnice vepsaná
Protože je průsečík os úhlů stejně vzdálen od všech tří stran trojúhelníka, můžeme zkonstruovat kružnici, pro niž budou strany trojúhelníku tečnami. Taková kružnice má střed Sv, poloměr d(Sv, AB) a nazývá se vepsaná, značíme kv. Body dotyku vepsané kružnice s jednotlivými stranami značíme Ta, Tb, Tc.
