Riešte rovnice s neznámou
t \in \mathbb{R}:
1.
\cos 3t=1
2.
\sqrt{2}\cos(4\pi+2t)=-1
-
\cos(4\pi+2t)=-\frac{1}{\sqrt{2}}
-
\cos(4\pi+2t)=-\frac{\sqrt{2}}{2}
- Zavedieme substitúciu
y=4\pi +2t.
-
\cos y=-\frac{\sqrt{2}}{2}
-

- Z grafu je vidieť, že
y_1=\frac {3}{4}{\pi} +2k\pi; y_2=\frac{5}{4}{\pi} +2k{\pi}, k \in \mathbb{Z}.
- Vrátime sa k substitúcii a v prvom prípade dostávame
4\pi +2t_1=\frac {3}{4}{\pi} +2k\pi
-
t_1=-\frac {13}{8}{\pi} +k\pi
(Prvé riešenie.)
- V druhom prípade platí:
4\pi +2t_2=\frac {5}{4}{\pi} +2k\pi
-
t_2=-\frac {11}{8}{\pi} +k\pi
(Druhé riešenie.)
- Výsledným množinu zapíšeme v tvare
K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{-13}{8}{\pi}+k\pi; \frac{-11}{8}{\pi}+k\pi \}\;.
3.
\cos (4\pi + \frac{\pi}{3})-\sqrt{3}=0
-
\cos (4\pi + \frac{\pi}{3})=\sqrt{3}
- Zavedieme substitúciu
y=4\pi+\frac{\pi}{3}
-
\cos y=\sqrt{3}
- Také y neexistuje, takže môžeme písať
y \in \emptyset.
4.
\sin(2t-\frac{\pi}{4})=\frac{\sqrt{2}}{2}
- Zavedieme substitúciu:
y=2t-\frac{\pi}{4}
-
\sin y = \frac{\sqrt{2}}{2}
-

- Z grafu a zo základných tabuľkových hodnôt funckie sínus plynie, že
x_1=\frac{\pi}{4}+2k\pi
- Vrátime sa k substitúcii
2t_1 -\frac{\pi}{4}=\frac{\pi}{4}+2k\pi
-
t_1=\frac{\pi}{4}+k\pi
(Prvé riešenie.)
-
2t_2 -\frac{\pi}{4}=\frac{3\pi}{4}+2k\pi
-
t_2=\frac{\pi}{2}+k\pi
(Druhé riešenie.)
- Výsledným riešením je množina
K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{\pi}{4}+k\pi; \frac{\pi}{2}+k\pi \}\;.
5.
{\rm tg}\: (1+t)=\frac{1}{\sqrt{3}}
-
{\rm tg}\: (1+t)=\frac{\sqrt{3}}{3}
- Zavedieme substitúciu:
y = 1+t
-
{\rm tg}\: y = \frac{\sqrt{3}}{3}
-
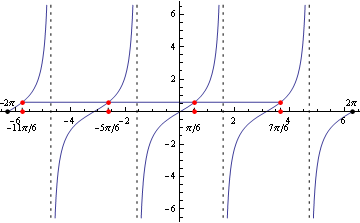
- Z grafu a zo základných tabuľkových hodnôt funckie tangens plynie:
y=\frac{\pi}{6}+k\pi
- Vrátime sa k substitúcii a úpravou postupne dostávame:
1+t=\frac{\pi}{6}+k\pi
-
t=\frac{\pi}{6}+k\pi-1
- Výsledným riešením je množina
K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{\pi}{6}+k\pi-1 \}\;.