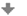Úlohy
Riešte rovnice s neznámou
t \in \mathbb{R}:
1.
\sin t = -1
- Využijeme graf funkcie sínus:
- Z grafu a z tabuľkových hodnôt plynie, že riešením je množina
K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{3\pi}{2}+2k\pi\}\;.
2.
\cos t= \frac {\sqrt{3}}{2}
- Využijeme graf funkcie kosínus:
- Z grafu a z tabuľkových hodnôt plynie, že riešením je množina
K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{\pi}{6}+2k\pi;\frac{11\pi}{6}+2k\pi\}\;.
3.
{\rm tg}\: t= \frac {\sqrt{3}}{3}
- Využijeme graf funkcie tangens:
- Z grafu a z tabuľkových hodnôt plynie, že riešením je množina
K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{\pi}{6}+k\pi\}\;.
4.
{\rm cotg}\: t= 1
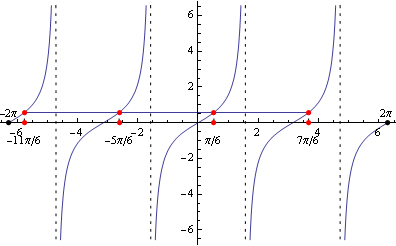
- Využijeme graf funkcie kotangens:
- Z grafu a z tabuľkových hodnôt plynie, že riešením je množina
K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{\pi}{4}+k\pi\}\;.
5.
2\frac{\large\cos t-1}{3}-4\frac{\large\cos t+1}{2}= -1 -\cos t
4\cos t -4-12\cos t -3= -6-6\cos t
-1= 2\cos t
\cos t= -\frac{1}{2}
Využijeme graf funkcie kosínus:
Z grafu a z tabuľkových hodnôt plynie, že riešením je množina
K = \bigcup\limits_{k\in\mathbb{Z}}\{\frac{2\pi}{3}+2k\pi;\frac{4\pi}{3}+2k\pi\}\;.
6. Riešte rovnicu s neznámou t a výsledok zapíšte v stupňovej miere s presnosťou na minúty:
\cos t = 0,242\ 5
Riešením je množina
K = \bigcup\limits_{k\in\mathbb{Z}}\{\ 75°58' + k\cdot360°; 284°02' + k\cdot360° \}\;.
7. Riešte rovnicu s neznámou t na intervale
\langle 0;2\pi\rangle
a výsledok zapíšte v oblúkovej miere s presnosťou na dve desatinné miesta:
\sin t = 0,987\ 6
Výsledkom je množina
\{\ 1,41; 1,73 \}\;.
