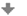Hyperbolometrické funkcie
Sú to funkcie y = {\rm argsinh}\: x (čítame argument hyperbolického sínusu), y = {\rm argcosh}\: x (čítame argument hyperbolického kosínusu), y = {\rm argtgh}\: x (čítame argument hyperbolického tangensu), y = {\rm argcotgh}\: x (čítame argument hyperbolického kotangensu), ktoré sú inverzné k hyperbolickým funkciam.
Definice
Funkcia y = {\rm argsinh}\: x je inverzná k funkcii x = \sinh y; je definovaná na \mathbb{R} . Teda: Ak x je reálne číslo, potom y = {\rm argsinh}\: x je to jednoznačne určené číslo y, pre ktoré \sinh y = x.
Definice
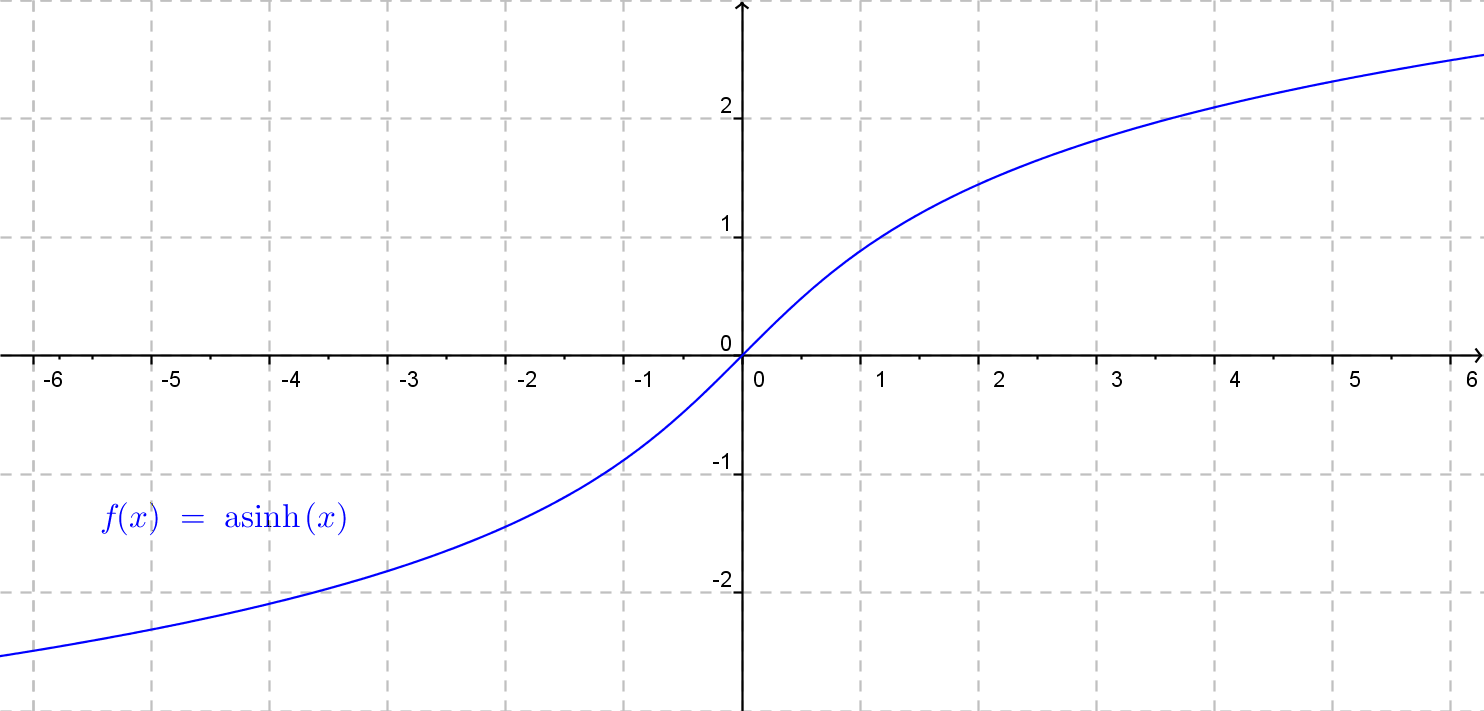
Funkcia y = {\rm argcosh}\: x je inverzná k funkcii x = \cosh x uvažovanej len na intervale <0, +\infty); je definovaná pre každé x z intervalu <-1, +\infty). Teda: Ak 1\leq x <\infty, , potom y = {\rm argcosh}\: x je to jednoznačne určené číslo y z intervalu <0, +\infty), pre ktoré \cosh y = x.
Definice
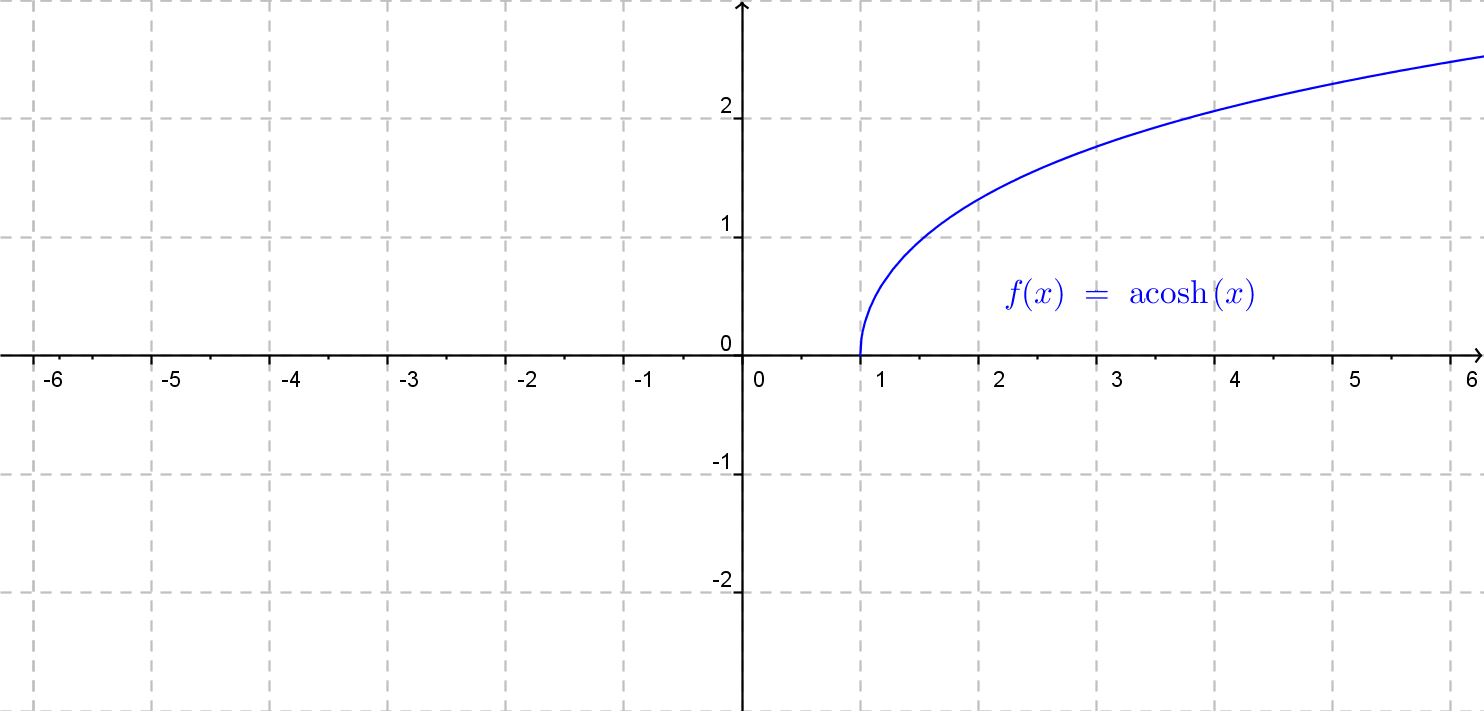
Funkcia y = {\rm argtgh}\: x je inverzná k funkcii x = {\rm tgh}\: y; je definovaná pre každé x z intervalu (-1, 1). Teda: Ak -1 < x < 1, potom y = {\rm argtgh}\: x je to jednoznačne určené číslo y, pre ktoré {\rm tgh}\: y = x.
Definice
Funkcia y = {\rm argcotgh}\: x je inverzná k funkcii x = {\rm cotgh}\: y; je definovaná pre každé x, pre ktoré |x| > 1. Teda: Ak |x| > 1, potom y = {\rm argcotgh}\: x je to jednoznačne určené číslo y, pre ktoré {\rm cotgh}\: y = x.
Základné vlastnosti hyperbolometrických funkcií
V tabuľke je uvedený prehľad základných vlastnosti hyperbolometrických funkcií.
|
Hyperbolometrická funkcia |
{\rm argsinh}\: x |
{\rm argcosh}\: x |
{\rm argtgh}\: x |
{\rm argcotgh}\: x |
|
Definičný obor |
\mathbb{R} |
\left \langle 1, \infty \right) |
(-1, 1) |
(-\infty, -1)\cup (1, \infty) |
|
Obor funkčných hodnôt |
\mathbb{R} |
\left \langle 0, \infty \right) |
\mathbb{R} |
(-\infty, 0)\cup (0, \infty) |
|
Monotónnosť |
rastúca na celom \mathbb{R} |
rastúca na intervale \left \langle 1, \infty \right) |
rastúca na intervale (-1, 1) |
klesajúca na intervale(-\infty, 0)\cup (0, \infty) |
Grafy hyperbolometrických funkcií a ďalších funkcií
Poznámka
Grafy hyperbolometrických funkcií sú vytvorené pomocou programu GeoGebra, kde sa používa iné značenie hyperbolometrických funkcií. Preto napríklad funkcia {\rm argtgh}\: x sa v GeoGebre značí ako {\rm atanh}\: x.Argument hyperbolického sínusu
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie argument hyperbolického sínusu.
Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/teoria.hyperbolometricke_funkcie.inc on line 360
Funkcia f(x)= a \cdot {\rm argsinh}\: x (b\cdot x + c) + d.
Poznámka
Grafy funkcií sú zobrazované pomocou apletu. V jednotlivých apletoch je možné pomocou posuvníkov meniť základné hodnoty parametrov a,b,c,d a všimnuť si tak správanie funkcií pri rôznych zmenách.
V tomto aplete pomocou posuvníkov môžme meniť základné hodnoty parametrov a,b,c,d.
Argument hyperbolického kosínusu
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie argument hyperbolického kosínusu.
Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/teoria.hyperbolometricke_funkcie.inc on line 414
Funkcia f(x)= a \cdot {\rm argcosh}\: x (b\cdot x + c) + d.
Argument hyperbolického tangensu
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie argument hyperbolického tangensu.
Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/teoria.hyperbolometricke_funkcie.inc on line 452
Funkcia f(x)= a \cdot {\rm argtgh}\: x (b\cdot x + c) + d.
Argument hyperbolického kotangensu
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie argument hyperbolického kotangensu.
Notice: Undefined variable: prefix in /srv/beegfs/web/web/kdm/diplomky/matus_kepic_dp/gon_rovnice_nerovnice/include/teoria.hyperbolometricke_funkcie.inc on line 490
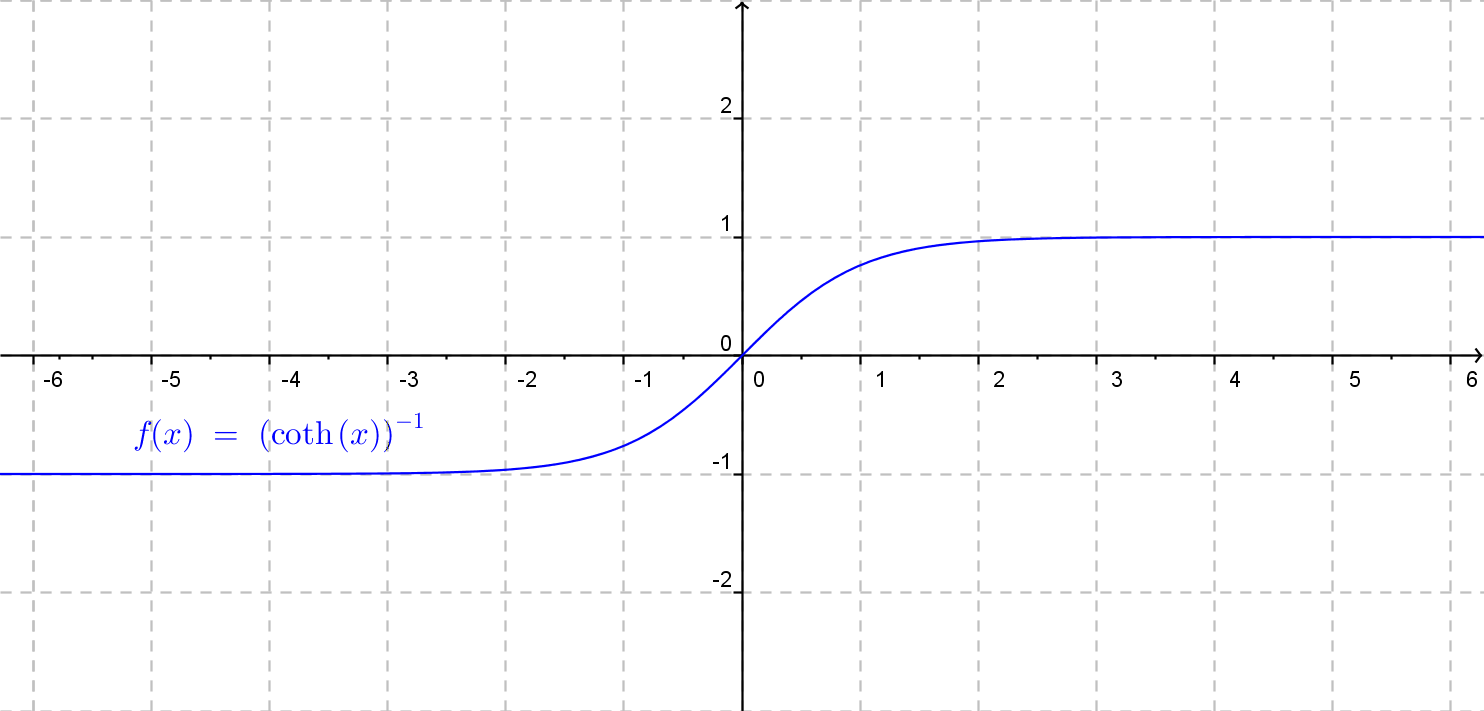
Funkcia f(x)= a \cdot {\rm argcotgh}\: x (b\cdot x + c) + d.
