Riešte rovnice s neznámou
t \in \mathbb{R}:
1.
\sin t \leq {\large \sqrt{2} \large \over \large 2}
2.
2\sqrt{3} \cos t \geq 3
4.
3\sqrt {3} {\rm tg}\: t - 3 \geq 0
5.
\cos t < \cos {\large\pi \over 4}
\cos t < {\sqrt {2} \over 2}
(Použili sme tabuľkovú hodnotu funkcie kosínus.)
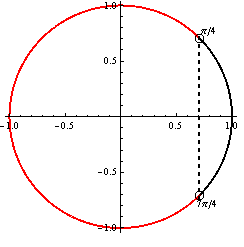
Využitím jednotkovej kružnice a periodicity funkcie kosínus dostávame výsledné riešenie, ktoré zapíšeme v tvare:
K = \bigcup\limits_{k\in\mathbb{Z}} \left (\frac{\pi}{4} + 2k\pi; \frac{7}{4}{\pi}+2k\pi \right).