Goniometrické rovnice a nerovnice

Úlohy

Riešte nerovnice s neznámou t \in \mathbb{R}:

1. \cos \left (3t - {\large \pi \over 2} \right) > {\sqrt{2} \over 2}

• Zavedieme substitúciu y = 3t - {\large \pi \over 2}.
• \cos y > {\sqrt{2} \over 2}
• 
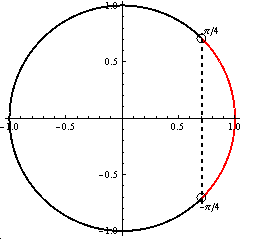
• Z jednotkovej kružnice je vidieť, že riešenim je y \in \left (-{\large \pi \over 4} + 2k\pi; {\large \pi \over 4} + 2k\pi \right), k \in \mathbb{Z}.
• Vrátime sa k substitúcií y = 3t - {\large \pi \over 2}.
• 3t \in \left({\large \pi \over 4} + 2k\pi; {3 \over 4}\pi + 2k\pi \right ) \Rightarrow t \in \left({\large \pi \over 12} + {2 \over 3}k\pi; {\large \pi \over 4} + {2 \over 3}k\pi \right ), k \in \mathbb{Z}.
• Výsledné riešenie zapíšeme v tvare K = \bigcup\limits_{k\in\mathbb{Z}} \left({\large \pi \over 12} + {2 \over 3}k\pi; {\large \pi \over 4} + {2 \over 3}k\pi \right ).

2. |\sin t| < \cos {\large \pi \over 6}

• |\sin t| < {\sqrt {3} \over 2} (Použili sme tabuľkovú hodnotu funkcie kosínus uvedenú v časti.)
• \sin t > -{\sqrt{3} \over 2} \vee \sin t < {\sqrt{3} \over 2} (Riešenie určíme pomocou jednotkovej kružnice, pričom využívame periodičnosť.)
• 
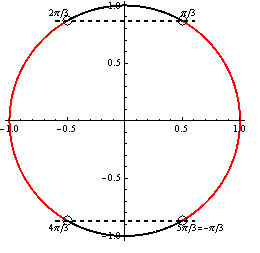
• Časť grafu vyznačená červenou farbou znázorňuje riešenie. Výsledné riešenie zapíšeme v tvare K = \bigcup\limits_{k\in\mathbb{Z}} \left(-{\large \pi \over 3} + k\pi; {\large \pi \over 3} + k\pi \right ).

3. {\rm tg}\: t \geq {\rm cotg}\: t

• Aby výrazy v nerovnici boli definované, musia platiť podmienky: x \not= {\large \pi \over 2} + k\pi \wedge x \not= k\pi, k \in \mathbb{Z}
• 
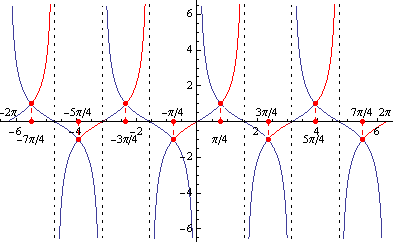
• Časť grafu vyznačená červenou farbou znázorňuje riešenie. Využitím periodičnosti dostávame riešenie, ktoré zapíšeme v tvare K = \bigcup\limits_{k\in\mathbb{Z}} \Big\{\left \langle {\large \pi \over 4} + k\pi; {\large \pi \over 2} + k\pi \right ) \cup \left \langle {3\ \over 4}\large \pi + k\pi; \pi + k\pi\right)\Big\}\

4. \sin 2t \leq \cos t

• 2\sin t \cos t - \cos t \leq 0 (Používame vzorce uvedené v časti.)
• \cos t (2 \sin t - 1) \leq 0 (Využijeme vlastnosť, kedy je súčin dvoch čísel menší, rovný ako nula).
• \cos t (2 \sin t - 1) \leq 0 \Leftrightarrow (\cos t \leq 0 \wedge 2 \sin t - 1 \geq 0) \vee (\cos t \geq 0 \wedge 2 \sin t - 1 \leq 0)
• Prvá možnosť: \cos t \leq 0 \wedge 2 \sin t - 1 \geq 0
• \cos t \leq 0
• 
• t_1 \in \left \langle {\pi \over 2} + 2k\pi; {3 \over 2}\pi + 2k\pi \right \rangle, k \in \mathbb{Z}
• K_{11} = \bigcup\limits_{k\in\mathbb{Z}} \left \langle {\pi \over 2} + 2k\pi; {3 \over 2}\pi + 2k\pi \right \rangle
• 2 \sin t - 1 \geq 0
• \sin t \geq {1 \over 2}
• 
• t_2 \in \left \langle {\pi \over 6} + 2k\pi; {5 \over 6}\pi + 2k\pi \right \rangle, k \in \mathbb{Z}
• K_{12} = \bigcup\limits_{k\in\mathbb{Z}} \left \langle {\pi \over 6} + 2k\pi; {5 \over 6}\pi + 2k\pi \right \rangle
• K_{1} = K_{11} \cap K_{12}
• K_{1} = \bigcup\limits_{k\in\mathbb{Z}} \left \langle {\pi \over 2} + 2k\pi; {5 \over 6}\pi + 2k\pi \right \rangle
• Druhá možnosť: \cos t \geq 0 \wedge 2 \sin t - 1 \leq 0
• \cos t \geq 0
• 
• t_3 \in \left \langle -{\pi \over 2} + 2k\pi; {\pi \over 2} + 2k\pi \right \rangle, k \in \mathbb{Z}
• K_{21} = \bigcup\limits_{k\in\mathbb{Z}} \left \langle -{\pi \over 2} + 2k\pi; {\pi \over 2} + 2k\pi \right \rangle
• 2\sin t - 1 \leq 0
• \sin t \leq {1 \over 2}
• 
• t_4 \in \left \langle -{5 \over 6}\pi + 2k\pi; {\pi \over 6} + 2\pi + 2k\pi \right \rangle, k \in \mathbb{Z}
• K_{22} = \bigcup_{k\in\mathbb{Z}} \left \langle -{5 \over 6}\pi + 2k\pi; {\pi \over 6}+ 2\pi + 2k\pi \right \rangle
• K_{2} = K_{21} \cap K_{22}
• K_{2} = \bigcup\limits_{k\in\mathbb{Z}} \left \langle -{\pi \over 2} + 2k\pi; {\pi \over 6} + 2k\pi \right \rangle
• K = K_{1} \cup K_{2} (Celkové riešenie je zjednotením obidvoch rozobratých možnosti.)

• Výsledné riešenie zapíšeme v tvare

  K = \bigcup\limits_{k\in\mathbb{Z}} \Big\{\left \langle -{\large \pi \over 2} + 2k\pi; {\large \pi \over 6} + 2k\pi \right \rangle \cup \left \langle {\large \pi \over 2} + 2k\pi; {5 \over 6} \pi + 2k\pi\right \rangle \Big\}.

5. \cos^2 t + 3\sin t - 3 \leq 0

• 1 - \sin^2 t + 3\sin t - 3 \leq 0 (Používame vzorce uvedené v časti.)
• -\sin^2 t + 3\sin t -2 \leq 0
• \sin^2 t - 3\sin t +2 \geq 0
• Zavedieme substitúciu \sin t = a
• a^2 -3a + 2 \geq 0 (Určíme diskriminant a korene odpovedajúcej kvadratickej rovnice.)
• D = (-3)^2 -4.1.2 = 1
• a_{1,2} = {-3 +- {\sqrt {1}} \over 2} \Rightarrow a_1 = 2; a_2 = 1 (Nájdené korene využijeme k tomu, aby sme kvadratický trojčlen v nerovnici rozložili na súčin.)
• (a-2).(a-1) \geq 0
• Vrátime sa k substitúcií a dostávame, že (\sin t - 2).(\sin t -1) \geq 0
• (\sin t -2).(\sin t -1) \geq 0 \Leftrightarrow \sin t -2 \leq 0 \wedge \sin t - 1 \leq 0 \vee \sin t - 2 \geq 0 \wedge \sin t - 1 \geq 0
• Prvá možnosť: \sin t - 2 \leq 0 \wedge \sin t - 1 \leq 0
• \sin t \leq 2 \wedge \sin t \leq 1
• K_1 = R (Plynie z vlastností funkcie sínus.)
• Druhá možnosť: \sin t -2 \geq 0 \wedge \sin t - 1 \geq 0
• \sin t \geq 2 \wedge \sin t \geq 1
• K_2 = \emptyset (Plynie z oboru funkčných hodnôt funkcie sínus.)
• K = K_1 \cup K_2 (Celkové riešenie je zjednotením obidvoch rozobratých možnosti.)
• Výsledné riešenie zapíšeme v tvare K = R.