Pak
$
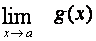 a platí
a platí
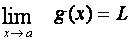 .
.
Tato věta
se občas nazývá větou o strážích, o policistech
či větou o třech limitách.
|
 |
 |
Myšlenka věty:
Když jsou na nějakém prstencovém okolí bodu a splněny
nerovnosti f(x) £
g(x) £ h(x)
a limity funkcí f a h jsou v bodě a rovny hodnotě
L, pak můžeme ihned říci, čemu se rovná limita funkce g v bodě a.
|
Věta:
Nechť
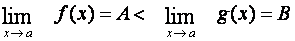 .
.
Pak
$d>0
"xÎP(a,d)
f(x) <
g(x).
|
 |
 |
Myšlenka věty: Když jsou hodnoty
limit funkcí f a g v bodě a v ostré nerovnosti, pak
víme, že existuje prstencové okolí bodu a, ve kterém jsou ve stejné
nerovnosti funkční hodnoty těchto funkcí.
|
Věta:
Nechť
existuje d>0
tak, že "xÎP(a,d)
f(x) £
g(x) a nechť 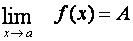 a
a
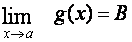 . Potom platí A
£
B.
. Potom platí A
£
B.
|
 |
 |
Myšlenka věty: Když existuje
nějaké prstencové okolí bodu a takové, že jsou v něm funkční
hodnoty funkcí f a g v neostré nerovnosti a když má funkce
f v bodě a limitu rovnu číslu A a funkce g
v bodě a limitu rovnu číslu B, pak víme, že pro tato čísla
(a tedy pro příslušné limity) platí stejná neostrá nerovnost.
|
|
 |
Věta je v jakémsi smyslu doplňkem k předchozí větě,
je ale nutné si uvědomit, že se v ní hovoří pouze o neostré nerovnosti. To
je podstatný rozdíl od předchozí věty.
|
Věta:
Nechť
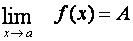 a AÎR.
a AÎR.
Potom
$d>0
tak, že funkce f je omezená na P(a,d).
Věta:
Nechť
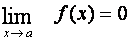 a
$d>0
tak, že funkce g(x) je omezená na P(a,d).
a
$d>0
tak, že funkce g(x) je omezená na P(a,d).
Pak
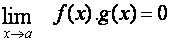 .
.
|
 |
 |
Myšlenka věty: Když je limita funkce f
v bodě a nulová a funkce g je na prstencovém okolí bodu a
omezená, pak ihned víme, že limita součinu těchto dvou funkcí v bodě a
je také nulová.
|
Věta:
Nechť
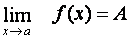 . Potom
. Potom
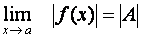 .
.
Věta:
Nechť
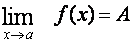 a
a
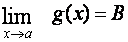 .
Potom
.
Potom
1.
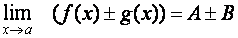
2.
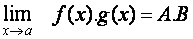
3.
Je-li B¹0
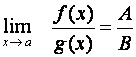
|
 |
 |
Myšlenka věty: Známe-li limity
funkcí f a g v bodě a, pak můžeme ihned určit limitu
součtu, rozdílu, součinu a s dodatečnou podmínkou také podílu funkcí f
a g.
|
Věta:
Nechť
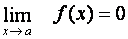 a
$d>0
xÎP(a,d)
Þ f(x)>0,
pak
a
$d>0
xÎP(a,d)
Þ f(x)>0,
pak 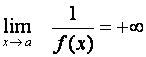 .
.
Věta:
Je-li
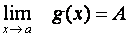 a funkce
f spojitá v bodě A, potom
a funkce
f spojitá v bodě A, potom
 .
.
|
 |
 |
Myšlenka věty: Limitu složené funkce f ○ g
můžeme spočítat tak, že spočteme limitu vnitřní funkce g
a výsledek dosadíme do vnější spojité funkce f.
|
Věta:
Nechť
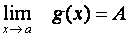 a
a
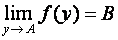 a
$d>0
xÎP(a,d)
Þ
g(x) ¹
A.
a
$d>0
xÎP(a,d)
Þ
g(x) ¹
A.
Potom
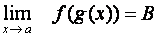 .
.
![]() a
$d>0
tak, že "xÎP(a,d)
f(x) = g(x).
a
$d>0
tak, že "xÎP(a,d)
f(x) = g(x).
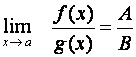
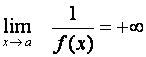 .
.