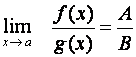|
Věta: Nechť
1.
2.
3. Je-li B¹0
|
Důkaz:
a. A, B Î R
Add 1.
Nechť je libovolně pevně zvoleno e >0.
$d1>0 "x xÎP(a,d1) Þ A-e/2 < f(x) < A+e/2
$d2>0 "x xÎP(a,d2) Þ B-e/2 < g(x) < B+e/2
Definujme d, d = min(d1,d2).
Pro každé xÎP(a,d) platí:
ê(f(x) ± g(x)) – (A±B)ú = ê(f(x) – A) ± (g(x) - B)ú £
£ êf(x) – Aú +êg(x) - Bú < e/2 + e/2 = e
Add 2.
Pozn. Důkaz předpokládá A¹0, pro A=0 se jedná o předchozí větu.
Protože funkce g má vlastní limitu, je tedy omezená na nějakém prstencovém okolí bodu a. Platí tedy
$K>0 $D>0 "xÎP(a,D) Þ êg(x)ú < K
Nechť je libovolně pevně zvoleno e >0.
$d1>0 "x xÎP(a,d1) Þ êf(x) - Aú < e/2K
$d2>0 "x xÎP(a,d2) Þ êg(x) - Bú < e/2 êAú
Definujme d, d = min(D,d1,d2).
Pro každé xÎP(a,d) platí:
êf(x).g(x) – A.Bú = êf(x).g(x) – A.g(x) + A.g(x) -A.Bú £
£ ê(f(x) – A)ú .êg(x)ú + êg(x) - Bú .|A| <
< (e/2K).K + (e/2 |A|).|A| = e
Add 3.
Pomocná tvrzení
(a) Nechť
![]() .
Potom
$D>0
xÎP(a,D)
Þ
.
Potom
$D>0
xÎP(a,D)
Þ
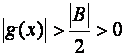
Důkaz (a)
Podle
předchozí věty je
![]()
Zvolme e, e = ú Bú/2. Je tedy e >0.
Z definice limity platí:
$D>0
xÎP(a,D)
Þ
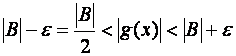
Konec důkazu.
(b) ![]() Þ
Þ
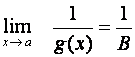
Důkaz (b)
Nechť je libovolně pevně zvoleno e >0.
Dle pomocného tvrzení (a) platí
$D>0
xÎP(a,D)
Þ
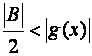
$d1>0
"x
xÎP(a,d1)
Þ
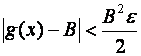
Definujme d, d = min(D,d1).
Pro každé xÎP(a,d) platí:
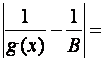
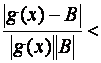
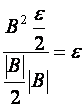
Konec důkazu.
Pomocí tvrzení (b) a předchozího bodu 2 o limitě součinu funkcí snadno získáme dokazované tvrzení.
Konec důkazu.
b. Případy s nevlastními limitami. Dokažme alespoň některé.
1.
Nechť je ![]() ,
,
![]() .
.
Pak platí
![]() .
.
Důkaz.
Nechť je libovolně pevně zvoleno K>0. Platí pak
$d1>0 "x xÎP(a,d1) Þ g(x) > K–A+1
Zvolme e, e = 1. Pak
$d2>0 "x xÎP(a,d2) Þ A-1 < f(x) < A+1
Definujme d, d = min(d1,d2).
Pro každé xÎP(a,d) platí:
f(x) +g(x) > A–1+K–A+1=K
Konec důkazu.
2.
Nechť je ![]() Ù
A>0
a
Ù
A>0
a
![]() .
.
Pak platí
![]()
Důkaz.
Z definice limity plyne
$d1>0 "x xÎP(a,d1) Þ A/2 < f(x)
Nechť je libovolně pevně zvoleno K<0.
Platí pak
$d2>0
"x
xÎP(a,d2)
Þ
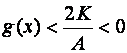
Definujme d, d = min(d1,d2).
Pro každé xÎP(a,d) pak platí:
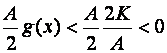
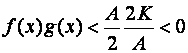
Platí tedy f(x).g(x) < K
Konec důkazu.