Úloha 8
| zobraz celé řešení | |
| << předchozí snímek | následující snímek>> |
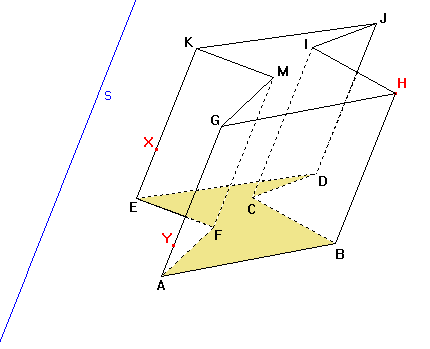 |
Zadání: Sestrojte řez kosého nekonvexního šestibokého hranolu ABCDEFGHIJKM rovinou HXY, kde bod X leží na hraně EK, bod Y leží na hraně AG. Při řešení úlohy využijeme osové afinity mezi rovinou řezu a rovinou dolní podstavy a za směr afinity s vezmeme směr bočních hran.
Nejprve musíme najít osu afinity, která je průsečnicí roviny dolní podstavy a roviny řezu dané body HXY.
K sestrojení osy afinity budeme potřebovat dva body. Jeden bod získáme pomocí bodů H, X. Obrazem přímky HX je přímka BE, protože obrazem bodu H je bod B a bodu X je bod E. Průsečíkem přímky HX a přímky BE je samodružný bod P, který bude ležet na ose afinity.
Druhý bod získáme pomocí bodů H, Y.
Obrazem přímky HY je přímka BA, protože obrazem bodu H je bod B a bodu Y je bod A. Průsečíkem přímky HY a přímky BA je samodružný bod Q, který bude ležet na ose afinity.
Pomocí bodů P, Q již můžeme sestrojit osu afinity o.
Sestrojíme bod řezu T na hraně JK. Bod R je průsečík přímky DE s osou o. Vzorem přímky DE je přímka XR a tedy průsečík přímky XR s hranou JK je bod řezu T.
Body řezu TH leží v jedné rovině, v rovině horní podstavy. Můžeme tedy sestrojit bod řezu U, který je průsečíkem přímky TH a hrany IJ.
Sestrojíme bod řezu V na hraně FM. Bod S je průsečík přímky EF s osou o. Vzorem přímky EF je přímka XS a tedy průsečík přímky XS s hranou FM je bod řezu V.
Obdobně sestrojíme bod řezu W na hraně CI pomocí bodu U a přímky CD.
Nyní známe všechny vrcholy mnohoúhelníku, který je řezem, a strany tohoto mnohoúhelníku jsou hranicemi řezu v příslušných stěnách.
|
zobraz řešení interaktivně
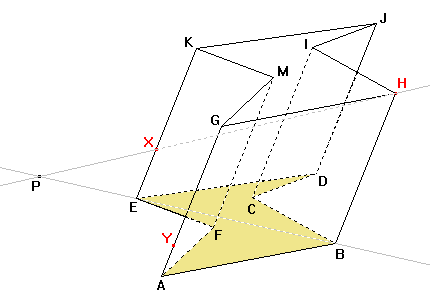 |
Nejprve musíme najít osu afinity, která je průsečnicí roviny dolní podstavy a roviny řezu dané body HXY. K sestrojení osy afinity budeme potřebovat dva body. Jeden bod získáme pomocí bodů H, X. Obrazem přímky HX je přímka BE, protože obrazem bodu H je bod B a bodu X je bod E. Průsečíkem přímky HX a přímky BE je samodružný bod P, který bude ležet na ose afinity. |
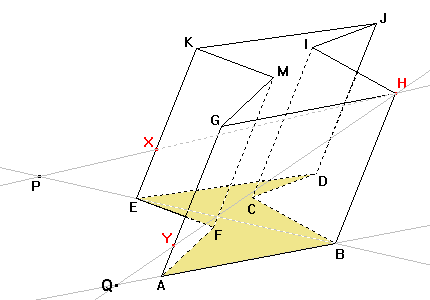 |
Druhý bod získáme pomocí bodů H, Y. Obrazem přímky HY je přímka BA, protože obrazem bodu H je bod B a bodu Y je bod A. Průsečíkem přímky HY a přímky BA je samodružný bod Q, který bude ležet na ose afinity. |
 |
Pomocí bodů P, Q již můžeme sestrojit osu afinity o. |
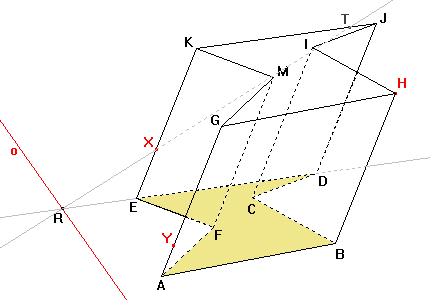 |
Sestrojíme bod řezu T na hraně JK. Bod R je průsečík přímky DE s osou o. Vzorem přímky DE je přímka XR a tedy průsečík přímky XR s hranou JK je bod řezu T. |
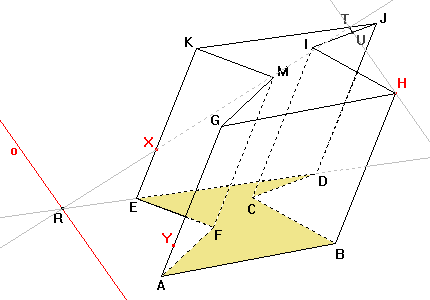 |
Body řezu TH leží v jedné rovině, v rovině horní podstavy. Můžeme tedy sestrojit bod řezu U, který je průsečíkem přímky TH a hrany IJ. |
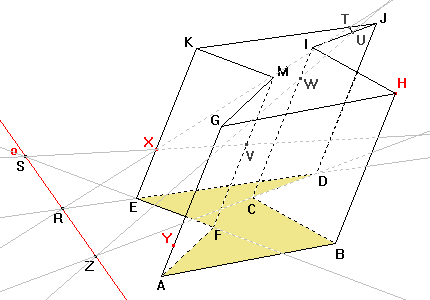 |
Sestrojíme bod řezu V na hraně FM. Bod S je průsečík přímky EF s osou o. Vzorem přímky EF je přímka XS a tedy průsečík přímky XS s hranou FM je bod řezu V. Obdobně sestrojíme bod řezu W na hraně CI pomocí bodu U a přímky CD. |
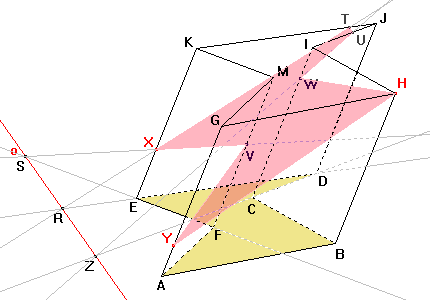 |
Nyní známe všechny vrcholy mnohoúhelníku, který je řezem, a strany tohoto mnohoúhelníku jsou hranicemi řezu v příslušných stěnách. |